Ecuación general de la elipse
La forma de la elipse es ovalada y el área de una elipse está definida por su eje mayor y su eje menor. Área de la elipse = πab, donde a y b son la longitud de los semiejes mayor y menor de una elipse. La elipse es similar a otras partes de la sección cónica, como la parábola y la hipérbola, que son de forma abierta y sin límites.
Una elipse si hablamos en términos de locus, es el conjunto de todos los puntos de un plano XY, cuya distancia a dos puntos fijos (conocidos como focos) suma un valor constante.
La elipse es una de las secciones cónicas, que se produce, cuando un plano corta al cono en un ángulo con la base. Si el cono es cortado por el plano, paralelo a la base, entonces forma un círculo.
Forma de elipse
En geometría, una elipse es una forma bidimensional que se define a lo largo de sus ejes. Una elipse se forma cuando un cono es intersecado por un plano en un ángulo con respecto a su base.
Tiene dos puntos focales. La suma de las dos distancias al punto focal, para todos los puntos de la curva, es siempre constante.
Un círculo es también una elipse, donde los focos están en el mismo punto, que es el centro del círculo.
La elipse se define por sus dos ejes a lo largo de los ejes x e y:
- Eje mayor
- Eje menor
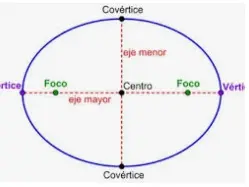
El eje mayor es el diámetro más largo de la elipse (normalmente denotado por «a»), que pasa por el centro de un extremo a otro, en la parte ancha de la elipse. El eje menor es el diámetro más corto de la elipse (denominado «b») y pasa por el centro en la parte más estrecha.
La mitad del eje mayor se llama semieje mayor y la mitad del eje menor se llama semieje menor.
Propiedades
- La elipse tiene dos puntos focales, también llamados focos.
- La distancia fija se llama directriz.
- La excentricidad de la elipse está comprendida entre 0 y 1. 0≤e<1
- La suma total de cada distancia desde el lugar de una elipse a los dos focos es constante
- La elipse tiene un eje mayor y un eje menor y un centro
Excentricidad de la elipse
La relación entre las distancias del centro de la elipse desde cualquiera de los dos focos al semieje mayor de la elipse se define como la excentricidad de la elipse.
La excentricidad de la elipse, e = c/a
Donde c es la distancia focal y a es la longitud del semieje mayor.
Como c ≤ a la excentricidad es siempre mayor que 1 en el caso de una elipse.
Además
c2 = a2 – b2
Por tanto, la excentricidad pasa a ser
e = √(a2 – b2)/a
e = √[(a2 – b2)/a2] e = √[1-(b2/a2)]
Vídeos de Ecuación general de la elipse
Contenido