Asintota horizontal
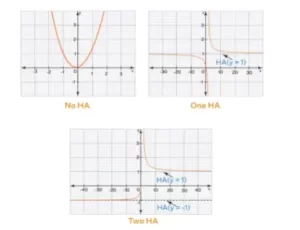
La asíntota horizontal de una función y = f(x) es una recta y = k cuando si lim ₓ→∞ f(x) = k o lim ₓ→ -∞ f(x) = k. es decir, es una recta a la que la gráfica (curva) de la función parece acercarse a medida que x→∞ o x→ -∞. Se suele denominar HA. Aquí, k es un número real al que se aproxima la función cuando el valor de x es extremadamente grande o extremadamente pequeño. Una función puede tener o no una asíntota horizontal. Pero el número máximo de asíntotas que puede tener una función es 2. Es decir, una función puede tener 0, 1 o 2 asíntotas. A continuación se muestran algunos ejemplos de asíntotas horizontales que nos darán una idea de cómo son. Una línea horizontal se suele representar con una línea horizontal punteada. Cuando el propio eje x es el HA, entonces no solemos utilizar la línea punteada para ello.
Hay que tener en cuenta que el HA lo encontramos al graficar una curva sólo para representar el valor al que se aproxima la función. Pero no es obligatorio dibujarla al graficar la curva porque NO es parte de la curva. Incluso las calculadoras gráficas no muestran una línea horizontal para la asíntota horizontal. En otras palabras, una línea horizontal es una línea imaginaria.
¿Puede una asíntota horizontal cruzar la curva?
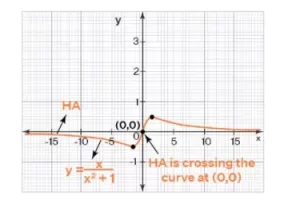
Sí, una asíntota horizontal y = k de una función y = f(x) puede cruzar la curva (gráfica), es decir, puede existir un valor de x tal que f(x) = k. Ten en cuenta que éste NO es el caso de ninguna asíntota vertical, ya que una asíntota vertical nunca cruza la curva. Aquí hay un ejemplo en el que la asíntota horizontal (HA) interseca la curva.
Aquí, la curva tiene una asíntota horizontal como eje x (cuya ecuación es y = 0) y cruza la curva en (0, 0). Intenta resolver la ecuación x/(x2+1) = 0 y obtendremos x = 0.
¿Cómo encontrar la asíntota horizontal?
Estos son los pasos para encontrar la asíntota horizontal de cualquier tipo de función y = f(x).
Paso 1: Encontrar lim ₓ→∞ f(x). es decir, aplicar el límite de la función como x→∞.
Paso 2: Encuentra lim ₓ→ -∞ f(x). es decir, aplica el límite para la función como x→ -∞.
Paso 3: Si alguno (o ambos) de los límites anteriores son números reales entonces represente la asíntota horizontal como y = k donde k representa el valor del límite.
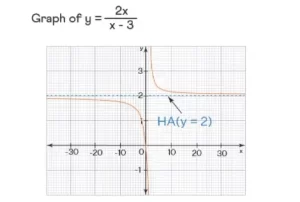
Si alguno (o ambos) de los casos anteriores dan ∞ o -∞ como respuesta, entonces simplemente ignóralos y NO son las asíntotas horizontales. A veces, cada uno de los límites puede dar el mismo valor y en ese caso (como en el siguiente ejemplo), sólo tenemos una HA.
De hecho, utilizamos la asíntota horizontal para encontrar el rango de una función racional. Sólo utilizamos el hecho de que la HA NO es una parte de la gráfica de la función. De la gráfica anterior, el rango de f(x) es {y ∈ R | y ≠ 2}.
Vídeos de Asintota horizontal
https://www.youtube.com/watch?v=P7m-u3IuAFY
Contenido