Teorema de la tangente
En geometría, una tangente es la línea que se traza desde un punto externo y pasa por un punto de la curva. Un ejemplo de la vida real de una tangente es cuando se monta en bicicleta, cada punto de la circunferencia de la rueda hace una tangente con la carretera.
Definición de tangente: La tangente en geometría se define como una línea que toca una curva o una superficie curva exactamente en un punto.
Tangente de una circunferencia
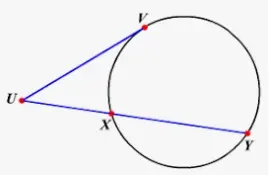
Una tangente de un círculo se define como una línea recta que toca o interseca el círculo en un solo punto. Una tangente es una línea que nunca entra en el interior del círculo. La siguiente figura muestra una circunferencia con un punto P. Se ha dibujado una tangente L que pasa por P. Este es un ejemplo de tangente a una circunferencia.
Punto de tangencia
El punto de tangencia se define como el único punto de intersección en el que la recta toca o interseca a la circunferencia. En la figura anterior, el punto P representa el punto de tangencia.
Propiedades de la tangente
La tangente tiene dos propiedades importantes:
- Una tangente toca a una curva en un solo punto.
- Una tangente es una línea que nunca entra en el interior del círculo.
- La tangente toca el radio de la circunferencia en el punto de tangencia en un ángulo recto.
- Aparte de las propiedades mencionadas, la tangente al círculo tiene teoremas matemáticos asociados y estos teoremas se utilizan al hacer cálculos importantes en geometría. Veamos algunos teoremas de las tangentes al círculo en detalle.
Teoremas de la tangente
Hay dos teoremas muy importantes sobre la tangente a un círculo. Son el teorema de la tangente al radio y el teorema de las dos tangentes. Vamos a discutir sus enunciados y su demostración en detalle.
Teorema de la tangente al radio: La tangente en cualquier punto de una circunferencia es perpendicular al radio por el punto de contacto.
Dada: La tangente PL a una circunferencia S (con centro de circunferencia O), y el punto de contacto es A.
Demostrar: OA es perpendicular a la tangente PL.
Teorema del radio de la tangente
Demostración: El punto P queda fuera de la circunferencia. Al unir PO obtenemos PO > OA (radio de una circunferencia). Esta condición se aplicará a todos los puntos de la recta PL excepto al punto A.
PO > OA demuestra que OA es la menor de todas las distancias del punto O a los demás puntos de PL.
Por tanto, se demuestra que OA es perpendicular a PL.
Teorema de las dos tangentes: Supongamos que se trazan dos tangentes a una circunferencia desde un punto exterior C. Sean los puntos de contacto A y B, como se muestra en la imagen siguiente.
El teorema dice lo siguiente:
- Las longitudes de estas dos tangentes serán iguales, es decir, CA = CB.
- Las dos tangentes subtendrán ángulos iguales en el centro, es decir, ∠COA = ∠COB.
- El ángulo entre las tangentes será bisecado por la recta que une el punto exterior y el centro, es decir, ∠ACO = ∠BCO.
Demostración: Las tres partes quedarán demostradas si mostramos que ΔCAO es congruente con ΔCBO. Comparando los dos triángulos, vemos que:
OA = OB (radios de la misma circunferencia)
OC = OC (lado común)
∠OAC = ∠OBC = 90° (La tangente trazada a una circunferencia es perpendicular al radio en el punto de tangencia)
Así pues, por el criterio de la RHS, ΔCAO es congruente con ΔCBO, y se deduce la verdad de las tres afirmaciones.
Vídeos de Teorema de la tangente
Contenido