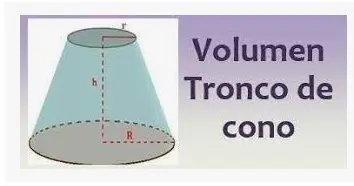
Volumen de tronco de cono
Los dos extremos circulares de un cono truncado se llaman bases. Al radio de la base circular más pequeña lo llamaremos radio pequeño y lo representaremos con r, y al radio de la base circular más grande lo llamaremos radio grande y lo representaremos con R. La distancia entre los centros de las dos bases se llama altura del cono truncado y la representamos con h. Por último, la distancia más corta entre las aristas exteriores de las bases se llama altura de la inclinación y la representamos con s.
Volumen de un cono truncado
Supongamos que vas al cine y pides unas palomitas grandes. Te mueres de ganas de hincarle el diente a esa delicia salada y mantecosa, pero antes de hacerlo, empiezas a preguntarte cuántas palomitas caben dentro de la tarrina grande de palomitas. Tengo una noticia para ti. En realidad te estás preguntando cuál es el volumen de la tarrina de palomitas.
El volumen de un cono truncado es la cantidad de espacio dentro del cono truncado. La buena noticia es que tenemos una bonita fórmula que podemos utilizar para encontrar el volumen de un cono truncado.
Volumen = (1/3) ⋅ π ⋅ h(R 2 + r 2 + R ⋅ r)
Como te pica la curiosidad, le pides al empleado del mostrador de las concesiones que te muestre una tarrina grande de palomitas vacía. Cuando te la da, tomas algunas medidas rápidas y descubres que el radio grande es de 5 pulgadas, el radio pequeño es de 4 pulgadas, la altura es de 10 pulgadas y la altura oblicua es de 11 pulgadas. Le devuelves la cubeta vacía al trabajador de la concesión y sacas un lápiz y un papel para calcular el volumen de la cubeta grande de palomitas utilizando tu fórmula.
Ejemplos de volumen de un cono parcial
- La base y el radio superior de un cono parcial son 3 mm y 6 mm respectivamente. Si la altura es de 100 mm, encuentra el volumen del cono parcial. (Usa π = 3.14)
Solución:
Dada,
Altura del cono parcial, h = 100 mm
Radio de la parte superior, r = 3 mm
Radio de la parte inferior, R = 6 mm
El volumen del cono parcial, V = 1/3 × πh(R2 + Rr + r2)
o bien, V = 1/3 × 3,14 × 100 × (62 + 6 × 3 + 32)
⇒ V = 1/3 × 314 × (36 + 18 + 9)
⇒ V = 1/3 × 314 × 63
⇒ V = 314 × 21
⇒ V = 6.594 mm3
Respuesta: El volumen de un cono parcial es de 6.594 mm3
- James va a rellenar con jarabe de chocolate seis conos formados por galletas. Cada cono tiene una altura de 24 cm y una altura oblicua de 25 cm, halla la cantidad total de jarabe de chocolate necesaria.
Solución:
Dada,
Altura del cono, H = 24 cm
Altura oblicua del cono, L = 25 cm
Hallemos primero el radio de la base ‘R’ del cono:
L2 = R2 + H2
⇒ R2 = L2 – H2
⇒ R2 = 252 – 242
⇒ R2 = 625 – 576 = 49
⇒ R = 7 cm
Volumen del jarabe de chocolate en un cono = 1/3 × πR2 × H
Volumen del jarabe de chocolate en seis conos = 6 × 1/3 × πR2 × H
= 2 × (22/7) × 72 × 24
= 2 × 22 × 7 × 24
= 7.392 cm3
Vídeos de Volumen de tronco de cono
Contenido