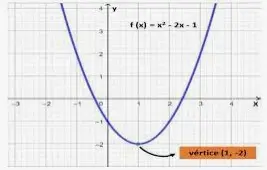
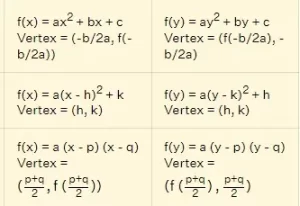Vertice de una parabola
Hallar el vértice de una parábola en forma estándar
Sabemos que la ecuación de una parábola en forma estándar puede ser de la forma y = ax2 + bx + c (arriba/abajo) o de la forma x = ay2 + by + c (izquierda/derecha). Veamos los pasos para encontrar el vértice de la parábola en cada caso.
Vértice de una parábola abierta arriba/abajo
Cuando una parábola se abre hacia arriba o hacia abajo, su ecuación en la forma estándar es de la forma y = ax2 + bx + c. Aquí están los pasos para encontrar el vértice (h, k) de tales parábolas. Los pasos se explican con un ejemplo en el que encontraremos el vértice de la parábola y = 2×2 – 4x + 1.
Paso – 1: Comparar la ecuación de la parábola con la forma estándar y = ax2 + bx + c.
Comparando y = 2×2 – 4x + 1 con la ecuación anterior, a = 2, b = -4, y c = 1.
Paso – 2: Encontrar la coordenada x del vértice utilizando la fórmula, h = -b/2a
Entonces obtenemos h = -(-4) / (2 × 2) = 1.
Paso – 3: Para encontrar la coordenada y (k) del vértice, sustituye x = h en la expresión ax2+ bx + c.
Entonces k = 2(1)2 – 4(1) + 1 = 2 – 4 + 1 = -1.
Paso – 4: Escribe el vértice (h, k) como un par ordenado.
El vértice = (h, k) = (1, -1).
Vértice de una parábola abierta a la izquierda/derecha
Cuando una parábola se abre a la izquierda o a la derecha, su ecuación en la forma estándar es de la forma x = ay2 + by + c. Aquí están los pasos para encontrar el vértice (h, k) de tales parábolas que se explican con un ejemplo donde vamos a encontrar el vértice de la parábola x = 2y2 – 4y + 1.
Paso – 1: Comparar la ecuación de la parábola con la forma estándar x = ay2 + by + c.
Comparando x = 2y2 – 4y + 1 con la ecuación anterior, a = 2, b = -4, y c = 1.
Paso – 2: Encontrar la coordenada y del vértice utilizando la fórmula, k = -b/2a
Entonces obtenemos k = -(-4) / (2 × 2) = 1.
Paso – 3: Para encontrar la coordenada x (h) del vértice, sustituye y = k en la expresión ay2+ by + c.
Entonces h = 2(1)2 – 4(1) + 1 = 2 – 4 + 1 = -1.
Paso – 4: Escribe el vértice (h, k) como un par ordenado.
El vértice = (h, k) = (-1, 1).
Vídeos de Vertice de una parabola
Contenido