Tipo de funciones
Función, en matemáticas, expresión, regla o ley que define una relación entre una variable (la variable independiente) y otra variable (la variable dependiente). Las funciones son omnipresentes en las matemáticas y son esenciales para formular relaciones físicas en las ciencias. La definición moderna de función fue dada por primera vez en 1837 por el matemático alemán Peter Dirichlet.
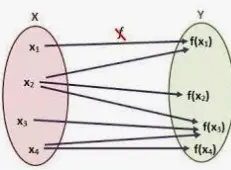
Si una variable y está tan relacionada con una variable x que siempre que se asigna un valor numérico a x, existe una regla según la cual se determina un valor único de y, entonces se dice que y es una función de la variable independiente x.
Esta relación se simboliza comúnmente como y = f(x) -que se dice «f de x»- e y y se relacionan de manera que para cada x, hay un valor único de y. Es decir, f(x) no puede tener más de un valor para la misma x. Para utilizar el lenguaje de la teoría de conjuntos, una función relaciona un elemento x con un elemento f(x) en otro conjunto. El conjunto de valores de x se llama dominio de la función, y el conjunto de valores de f(x) generado por los valores del dominio se llama rango de la función. Además de f(x), a menudo se utilizan otros símbolos abreviados como g(x) y P(x) para representar funciones de la variable independiente x, especialmente cuando la naturaleza de la función es desconocida o no está especificada.
Funciones comunes
Muchas fórmulas matemáticas muy utilizadas son expresiones de funciones conocidas. Por ejemplo, la fórmula del área de un círculo, A = πr2, da la variable dependiente A (el área) en función de la variable independiente r (el radio). Las funciones que implican más de dos variables (llamadas funciones multivariables o multivariadas) también son comunes en matemáticas, como puede verse en la fórmula del área de un triángulo, A = bh/2, que define A como una función tanto de b (base) como de h (altura). En estos ejemplos, las restricciones físicas obligan a que las variables independientes sean números positivos. Cuando se permite que las variables independientes también tomen valores negativos, es decir, cualquier número real, las funciones se denominan funciones de valor real.
La fórmula del área de un círculo es un ejemplo de función polinómica. La forma general de estas funciones es
P(x) = a0 + a1x + a2x2+⋯+ anxn,
donde los coeficientes (a0, a1, a2,…, an) están dados, x puede ser cualquier número real, y todas las potencias de x son números para contar (1, 2, 3,…). (Cuando las potencias de x pueden ser cualquier número real, el resultado se conoce como función algebraica). Las funciones polinómicas se han estudiado desde los primeros tiempos debido a su versatilidad: prácticamente cualquier relación en la que intervengan números reales puede ser aproximada por una función polinómica. Las funciones polinómicas se caracterizan por la mayor potencia de la variable independiente. Se suelen utilizar nombres especiales para las potencias de uno a cinco: lineal, cuadrática, cúbica, cuártica y quíntica, siendo las potencias más altas 1, 2, 3, 4 y 5, respectivamente.
Las funciones polinómicas se pueden representar geométricamente mediante la geometría analítica. La variable independiente x se representa a lo largo del eje x (una línea horizontal), y la variable dependiente y se representa a lo largo del eje y (una línea vertical). Cuando la gráfica de una relación entre x e y se traza en el plano x-y, la relación es una función si una línea vertical pasa siempre por un solo punto de la curva graficada; es decir, habría un solo punto f(x) correspondiente a cada x, que es la definición de una función. La gráfica de la función consiste entonces en los puntos con coordenadas (x, y) donde y = f(x). Por ejemplo, en la figura se muestra la gráfica de la ecuación cúbica f(x) = x3 – 3x + 2.
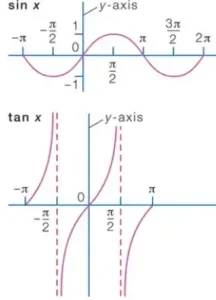
Otro tipo de función común que se ha estudiado desde la antigüedad son las funciones trigonométricas, como sen x y cos x, donde x es la medida de un ángulo (ver figura). Debido a su naturaleza periódica, las funciones trigonométricas se utilizan a menudo para modelar comportamientos que se repiten, o «ciclos».
Funciones complejas
Las aplicaciones prácticas de las funciones cuyas variables son números complejos no son tan fáciles de ilustrar, pero sin embargo son muy amplias. Se dan, por ejemplo, en electrotecnia y aerodinámica. Si la variable compleja se representa en la forma z = x + iy, donde i es la unidad imaginaria (la raíz cuadrada de -1) y x e y son variables reales (véase la figura), es posible dividir la función compleja en partes reales e imaginarias: f(z) = P(x, y) + iQ(x, y). Un punto en el plano complejo. A diferencia de los números reales, que pueden localizarse mediante un único número con signo (positivo o negativo) a lo largo de una recta numérica, los números complejos requieren un plano con dos ejes, uno para la componente de los números reales y otro para la componente imaginaria. Aunque el plano complejo se parece al plano ordinario de dos dimensiones, donde cada punto está determinado por un par ordenado de números reales (x, y), el punto x + iy es un solo número.
Funciones inversas
Intercambiando los papeles de las variables independiente y dependiente en una función dada, se puede obtener una función inversa. Las funciones inversas hacen lo que su nombre indica: deshacen la acción de una función para devolver una variable a su estado original. Así, si para una función dada f(x) existe una función g(y) tal que g(f(x)) = x y f(g(y)) = y, entonces g se denomina función inversa de f y se le da la notación f-1, donde por convención se intercambian las variables. Por ejemplo, la función f(x) = 2x tiene la función inversa f-1(x) = x/2.
Otras expresiones funcionales
Una función puede definirse mediante una serie de potencias. Por ejemplo, las ecuaciones de series infinitas se pueden utilizar para definir estas funciones para todos los valores complejos de x. Se pueden utilizar otros tipos de series y también productos infinitos cuando sea conveniente. Un caso importante es la serie de Fourier, que expresa una función en términos de senos y cosenos. Estas representaciones son de gran importancia en física, especialmente en el estudio del movimiento ondulatorio y otros fenómenos oscilatorios.
A veces, las funciones se definen más convenientemente por medio de ecuaciones diferenciales. Por ejemplo, y = sen x es la solución de la ecuación diferencial d2y/dx2 + y = 0 teniendo y = 0, dy/dx = 1 cuando x = 0; y = cos x es la solución de la misma ecuación teniendo y = 1, dy/dx = 0 cuando x = 0.
Vídeos de Tipo de funciones
Contenido