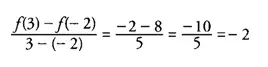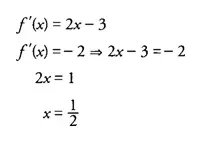Teorema de valor medio
El teorema del valor medio (MVT) es uno de los teoremas más frecuentes en la literatura de educación matemática. Es una de las herramientas más importantes utilizadas para demostrar muchos otros teoremas del cálculo diferencial e integral. A veces se enseña con su caso especial, el teorema de Rolle. El teorema de Rolle debe su nombre a Michel Rolle (1652-1719), un matemático francés que estableció el símbolo, ahora común, de la raíz enésima e insistió en que -a > -b, para a y b positivos, a < b. La hazaña iba en contra de las enseñanzas de Descartes y sentó las bases para la introducción de la omnipresente recta numérica.
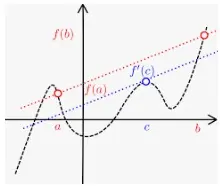
El teorema se enuncia como sigue. Si una función f(x) es continua en un intervalo cerrado [a,b] y diferenciable en un intervalo abierto (a,b), entonces existe al menos un número c ∈ (a,b) tal que:
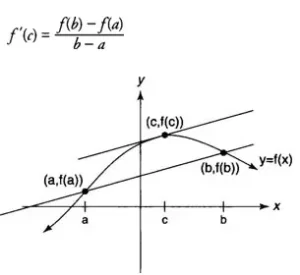
Geométricamente, esto significa que la pendiente de la recta tangente será igual a la pendiente de la recta secante que pasa por (a,f(a)) y (b,f(b)) para al menos un punto de la curva entre los dos puntos extremos. Obsérvese que para el caso especial en que f(a) = f(b), el teorema garantiza al menos un punto crítico, donde f(c) = 0 en el intervalo abierto ( a, b).
Ejemplo: Verificar la conclusión del Teorema del Valor Medio para f(x)= x 2-3 x-2 en [-2,3].
La función es continua en [-2,3] y diferenciable en (-2,3). La pendiente de la recta secante que pasa por los valores de los extremos es
La pendiente de la recta tangente es
Como ½ ∈ [-2,3], el valor de c al que se refiere la conclusión del Teorema del Valor Medio es c = ½
Demostración del teorema de Rolle
Sea k = f(a) = f(b). Consideramos tres casos:
f(x) = k para todo x ∈ (a, b).
Existe un x ∈ (a, b) tal que f(x) > k.
Existe un x ∈ (a, b) tal que f(x) < k.
Caso 1: Si f(x) = k para todo x ∈ (a, b), entonces f'(x) = 0 para todo x ∈ (a, b).
Caso 2: Como f es una función continua sobre el intervalo cerrado y acotado[a, b], por el teorema del valor extremo, tiene un máximo absoluto. Además, como hay un punto x ∈ (a, b) tal que f(x) > k, el máximo absoluto es mayor que k. Por tanto, el máximo absoluto no se da en ninguno de los extremos. Como resultado, el máximo absoluto debe ocurrir en un punto interior xc∈ (a, b). Como f tiene un máximo en un punto interior c, y f es diferenciable en c, por el teorema de Fermat, f'(c)=0.
Caso 3: El caso en que existe un punto x ∈ (a, b) tal que f(x) < k es análogo al caso 2, con el máximo sustituido por el mínimo.
Vídeos de Teorema de valor medio
Contenido