Relaciones trigonometricas
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos. La trigonometría se encuentra en toda la geometría, ya que toda forma de lados rectos puede descomponerse en un conjunto de triángulos. Además, la trigonometría tiene relaciones asombrosamente complejas con otras ramas de las matemáticas, en particular con los números complejos, las series infinitas, los logaritmos y el cálculo.
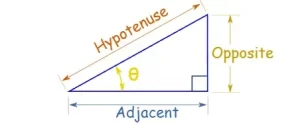
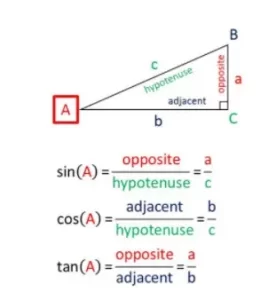
- La tangente del ángulo A = la longitud del lado opuesto dividida por la longitud del lado adyacente
- El seno del ángulo A = la longitud del lado opuesto dividida por la longitud de la hipotenusa
- El coseno del ángulo A = la longitud del lado adyacente dividida por la longitud de la hipotenusa
Formas que no son triángulos rectos
La trigonometría no se limita a los triángulos rectos. Se puede utilizar con todos los triángulos y todas las formas con lados rectos, que se tratan como un conjunto de triángulos. Para cualquier triángulo, a través de las seis medidas de los lados y los ángulos, si se conocen al menos tres, normalmente se pueden determinar los otros tres. De las seis configuraciones de tres lados y ángulos conocidos, sólo dos de estas configuraciones no se pueden utilizar para determinar todo sobre un triángulo: tres ángulos conocidos (AAA), y un ángulo conocido adyacente y opuesto a los lados conocidos (ASS). Las longitudes de los lados y los ángulos desconocidos se determinan con las siguientes herramientas:
- La Ley de los Senos, que dice que si se conocen las dos medidas de uno de los tres pares de ángulos/lados opuestos, los demás pueden determinarse a partir de una sola conocida: sen(A)/a = sen(B)/b = sen(C)/c
- La Ley de los Cosenos, que dice que un lado desconocido se puede encontrar a partir de dos lados conocidos y el ángulo entre ellos. Es esencialmente el Teorema de Pitágoras con un factor de corrección para los ángulos que no son de 90 grados: c2 = a2 + b2 – 2ab∙cos(C)
- El hecho de que todos los ángulos de un triángulo deben sumar 180 grados: A + B + C = 180°
Vídeos de Relaciones trigonometricas
Contenido