Máximos y mínimos derivadas
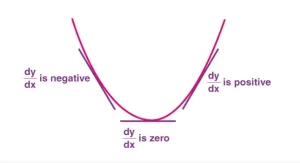
A continuación se muestra la figura de la curva con puntos estacionarios. Así se puede ver en la figura que antes de que la pendiente se haga cero era negativa, después de que se hace cero se hace positiva. Se puede decir que dy/dx es -ve antes del punto estacionario dy/dx es +ve después del punto estacionario. Por lo tanto se puede decir que d2 y/dx2 es positivo en el punto estacionario mostrado abajo, Por lo tanto se puede decir que dondequiera que la doble derivada es positiva es el punto de mínimo. Viceversa donde la doble derivada es negativa es el punto de máximos en la curva. Esto también se conoce como la prueba de la segunda derivada.
- Sea f una función definida en un intervalo abierto I.
- Sea f continua en un punto crítico c en I.
- Si f'(x) no cambia de signo a medida que x pasa por c, entonces c no es ni un punto de máximos locales ni un punto de mínimos locales. Dicho punto se denomina punto de inflexión.
Puntos estacionarios y puntos de inflexión
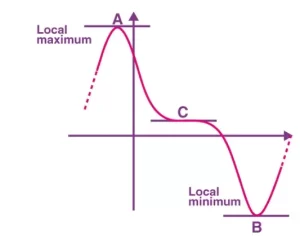
Los puntos estacionarios son los puntos en los que la pendiente de la gráfica se hace cero. En otras palabras, la tangente de la función se convierte en horizontal dy/dx = 0. Todos los puntos estacionarios vienen dados por la figura que se muestra a continuación A,B y C. Y los puntos en los que la función cambia su trayectoria si iba hacia arriba irá hacia abajo viceversa es decir, los puntos A y B son puntos de inflexión ya que la curva cambia su trayectoria. Pero el punto C no es punto de inflexión aunque la gráfica es plana durante un corto periodo de tiempo pero sigue bajando de izquierda a derecha.
Pruebas de derivadas
Las pruebas de derivadas ayudan a encontrar los máximos y mínimos de cualquier función. Normalmente, se utilizan las pruebas de derivadas de primer orden y de segundo orden. Veamos los detalles.
Prueba de la derivada de primer orden
Sea f la función definida en un intervalo abierto I. Y f sea continua en el punto crítico c en I tal que f'(c) = 0.
1. Si f'(x) cambia de signo de positivo a negativo a medida que x pasa por el punto c, entonces c es el punto de máximo local. Y la f(c) es el valor máximo.
2. Si f'(x) cambia de signo de negativo a positivo a medida que x pasa por el punto c, entonces c es el punto de mínimo local. Y la f(c) es el valor mínimo.
3. Si f'(x) no cambia de signo a medida que x pasa por c, entonces c no es ni un punto de máximos locales ni un punto de máximos locales. Se llamará punto de inflexión.
Prueba de la segunda derivada
Sea f la función definida en un intervalo I y es dos veces diferenciable en c.
i. x = c será un punto de máximo local si f'(c) = 0 y f»(c)<0. Entonces f(c) tendrá un valor máximo local.
ii. x = c será un punto de mínimo local si f'(c) = 0 y f»(c) > 0. Entonces f(c) tendrá un valor mínimo local.
iii. Cuando tanto f'(c) = 0 como f»(c) = 0 la prueba falla. Y esa prueba de la primera derivada te dará el valor de los máximos y mínimos locales.
Propiedades de los máximos y mínimos
1.Si f(x) es una función continua en su dominio, entonces al menos un máximo o un mínimo debe estar entre valores iguales de f(x).
2.Los máximos y los mínimos se producen alternativamente. Es decir, entre dos mínimos hay un máximo y viceversa.
3.Si f(x) tiende a infinito a medida que x tiende a a o b y f'(x) = 0 sólo para un valor x, es decir, c entre a y b , entonces f(c) es el mínimo y el menor valor. Si f(x) tiende a – ∞ cuando x tiende a a o b , entonces f(c) es el máximo y el mayor valor.
Vídeos de Máximos y mínimos derivadas
Contenido