Máximos y mínimos
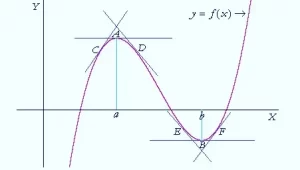
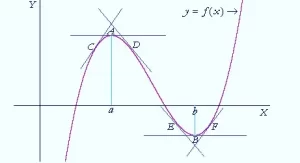
La tangente a la curva es horizontal. Lo vemos en los puntos A y B. La pendiente de cada recta tangente -la derivada cuando se evalúa en a o b- es 0.
f ‘(x) = 0.
Además, en los puntos inmediatamente a la izquierda de un máximo –en un punto C– la pendiente de la tangente es positiva: f ‘(x) > 0. Mientras que en los puntos inmediatamente a la derecha –en un punto D– la pendiente es negativa: f ‘(x) < 0.
En otras palabras, en un máximo, f ‘(x) cambia de signo de + a – .
En un mínimo, f ‘(x) cambia de signo de – a + . Podemos observar que en los puntos E y F.
También podemos observar que en un máximo, en A, la gráfica es cóncava hacia abajo. Mientras que en un mínimo, en B, es cóncava hacia arriba.
Un valor de x en el que la función tiene un máximo o un mínimo se llama valor crítico. En la figura —
— los valores críticos son x = a y x = b.
Los valores críticos determinan los puntos de inflexión, en los que la tangente es paralela al eje x. Los valores críticos — si los hay — serán las soluciones de f ‘(x) = 0.
Ejemplo de maximos y minimos
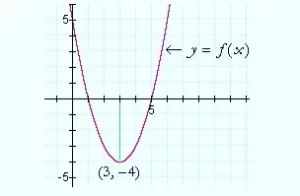
Sea f(x) = x2 – 6x + 5.
¿Hay algún valor crítico, algún punto de inflexión? Si es así, ¿determinan un máximo o un mínimo? ¿Y cuáles son las coordenadas en la gráfica de ese máximo o mínimo?
Solución. f ‘(x) = 2x – 6 = 0 implica x = 3.
x = 3 es el único valor crítico. Es la coordenada x del punto de inflexión. Para determinar la coordenada y, evalúe f en ese valor crítico — evalúe f(3):
f(x) = x2 – 6x + 5
f(3) = 32 – 6- 3 + 5
= -4.
El valor extremo es -4. Para ver si es un máximo o un mínimo, en este caso podemos simplemente mirar la gráfica.
Valores críticos
f(x) es una parábola, y podemos ver que el punto de inflexión es un mínimo.
Al encontrar el valor de x donde la derivada es 0, entonces, hemos descubierto que el vértice de la parábola está en (3, -4).
Pero no siempre podremos mirar la gráfica. La condición algebraica para un mínimo es que f ‘(x) cambie de signo de – a + . Esto lo vemos en los puntos E, B, F anteriores. El valor de la pendiente es creciente.
Ahora, decir que la pendiente es creciente, es decir que, en un valor crítico, la segunda derivada – que es la tasa de cambio de la pendiente – es positiva.
De nuevo, aquí está f(x):
f(x) = x2 – 6x + 5.
f ‘(x) = 2x – 6.
f »(x) = 2.
f » evaluada en el valor crítico 3 — f»(3) = 2 — es positiva. Esto nos dice algebraicamente que el valor crítico 3 determina un mínimo.
Condiciones suficientes
Valores extremos
Ahora podemos enunciar estas condiciones suficientes para los valores extremos de una función en un valor crítico a:
La función tiene un valor mínimo en x = a si f ‘(a) = 0
y f »(a) = un número positivo.
La función tiene un valor máximo en x = a si f ‘(a) = 0
y f »(a) = un número negativo.
En el caso del máximo, la pendiente de la tangente es decreciente: va de positivo a negativo. Podemos ver que en los puntos C, A, D.
Vídeos de maximos y minimos
Contenido