Matriz triangular superior

Una matriz es una matriz rectangular ordenada de números (o funciones). Un arreglo rectangular de m x n números (reales o complejos) en m filas y n columnas se llama matriz que tiene un orden de m por n. Se escribe como matriz m x n. La matriz se escribe con [ ] o ( ), que encierra la disposición. La matriz anterior se representa por A = [aij]mxn. Los números a11, a12, … etc., se conocen como los elementos de la matriz A, donde aij pertenece a la iª fila y a la jª columna y se llama el (i, j)º elemento de la matriz A = [aij].

Matriz triangular superior

Una matriz cuadrada en la que todos los elementos por encima de la diagonal son distintos de cero y por debajo de ella son cero se llama matriz triangular superior.

Una matriz triangular superior (o matriz triangular derecha) es un caso especial de una matriz cuadrada en la que todos los valores por debajo de la diagonal principal son ceros.

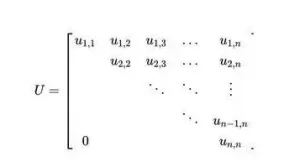
Se puede representar como

Las matrices triangulares, ya sean superiores o inferiores, son muy fáciles de resolver y se utilizan en diversos análisis numéricos.

Se representa como:

También puede llamarse matriz triangular derecha, ya que los términos no nulos se concentran en la derecha. También puede definirse como una matriz cuadrada que tiene entradas cero por debajo de la diagonal principal.

Propiedades de la matriz triangular superior

La suma de dos matrices triangulares superiores da una matriz triangular superior.
La sustracción de dos matrices triangulares superiores da una matriz triangular superior.
La inversa de la matriz triangular superior es una triangular superior.
La transposición de una matriz triangular superior será siempre una matriz triangular inferior, UT = L.
Incluso después de multiplicar cualquier cantidad escalar a una matriz triangular superior, la matriz seguirá siendo una matriz triangular superior.

¿Qué es una matriz triangular superior con un ejemplo?

Una matriz triangular superior es una matriz triangular con todos los elementos iguales por debajo de la diagonal principal. Es una matriz cuadrada con el elemento aij donde aij = 0 para todo j < i. Ejemplo de una matriz de 2×2. Nota: Las matrices triangulares superiores son matrices estrictamente cuadradas.

¿Cuál de las matrices es una matriz triangular superior?

En la disciplina matemática del álgebra lineal, una matriz triangular es un tipo especial de matriz cuadrada. Una matriz cuadrada se llama triangular inferior si todas las entradas por encima de la diagonal principal son cero. Del mismo modo, una matriz cuadrada se llama triangular superior si todas las entradas por debajo de la diagonal principal son cero.

¿Cuál es el ejemplo de matriz triangular?

En otras palabras, una matriz cuadrada es triangular superior si todas sus entradas por debajo de la diagonal principal son cero. Ejemplo de matriz triangular superior de 2 × 2: Una matriz cuadrada con elementos sij = 0 para j > i se denomina matriz triangular inferior.

Vídeos de Matriz triangular superior

Contenido