Intervalos de crecimiento y decrecimiento
Una función es «creciente» cuando el valor y aumenta a medida que aumenta el valor x, así:
Es fácil ver que y=f(x) tiende a aumentar a medida que avanza.
¿Plana?
¿Qué pasa con esa parte plana cerca del principio? ¿Está bien?
Sí, está bien cuando decimos que la función es crecientePero no está bien si decimos que la función es estrictamente creciente (no se permite el aplanamiento)
¿Qué pasa si no podemos trazar la gráfica para ver si es creciente? En ese caso necesitamos una definición usando el álgebra.
Para una función y=f(x):
cuando x1 < x2 entonces f(x1) ≤ f(x2) Creciente
cuando x1 < x2 entonces f(x1) < f(x2) Estrictamente Creciente
Eso tiene que ser cierto para cualquier x1, x2, no sólo para algunos bonitos que podamos elegir.
Las partes importantes son los signos < y ≤ … ¡recuerda dónde van!
Un ejemplo:
Esta también es una función creciente
aunque la tasa de incremento se reduce
Para un intervalo
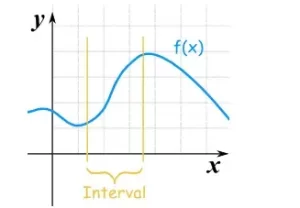
Normalmente sólo nos interesa algún intervalo, como éste:
Esta función es creciente para el intervalo indicado
(puede ser creciente o decreciente en otros lugares)
Funciones decrecientes
El valor y disminuye a medida que aumenta el valor x:
Para una función y=f(x):
cuando x1 < x2 entonces f(x1) ≥ f(x2) Decreciente
cuando x1 < x2 entonces f(x1) > f(x2) Estrictamente Decreciente
Observa que f(x1) es ahora mayor que (o igual a) f(x2).
Vídeos de Intervalos de crecimiento y decrecimiento
Contenido