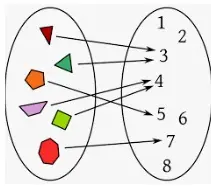
Función y relación
El concepto de función fue dado a conocer por los matemáticos en el siglo XVII. En 1637, el matemático y primer filósofo moderno, René Descartes, habló de muchas relaciones matemáticas en su libro Geometría. Sin embargo, el término «función» fue utilizado oficialmente por primera vez por el matemático alemán Gottfried Wilhelm Leibniz después de unos cincuenta años. Inventó una notación y = x para denotar una función, dy/dx, para denotar la derivada de una función. La notación y = f (x) fue introducida por el matemático suizo Leonhard Euler en 1734.
¿Qué es un conjunto?
Un conjunto es una colección de miembros o elementos distintos o bien definidos. En matemáticas, los miembros de un conjunto se escriben entre llaves o corchetes {}. Los miembros de los conjuntos pueden ser cualquier cosa, como por ejemplo; números, personas, o letras alfabéticas, etc.
Por ejemplo,
{a, b, c, …, x, y, z} es un conjunto de letras del alfabeto.
{…, -4, -2, 0, 2, 4, …} es un conjunto de números pares.
{2, 3, 5, 7, 11, 13, 17, …} es un conjunto de números primos
Se dice que dos conjuntos son iguales cuando contienen los mismos miembros. Consideremos dos conjuntos, A = {1, 2, 3} y B = {3, 1, 2}. Independientemente de la posición de los miembros en los conjuntos A y B, los dos conjuntos son iguales porque contienen miembros similares.
¿Qué son los números de pares ordenados?
Son números que van de la mano. Los números de pares ordenados se representan entre paréntesis y separados por una coma. Por ejemplo, (6, 8) es un número de par ordenado en el que los números 6 y 8 son el primer y segundo elemento, respectivamente.
¿Qué es un dominio?
Un dominio es un conjunto de todos los valores de entrada o primeros valores de una función. Los valores de entrada son generalmente los valores «x» de una función.
¿Qué es un rango?
El rango de una función es un conjunto de todos los valores de salida o segundos. Los valores de salida son los valores ‘y’ de una función.
¿Qué es una función?
En matemáticas, una función puede definirse como una regla que relaciona cada elemento de un conjunto, llamado dominio, con exactamente un elemento de otro conjunto, llamado rango. Por ejemplo, y = x + 3 e y = x2 – 1 son funciones porque cada valor de x produce un valor de y diferente.
Relación
Una relación es cualquier conjunto de números ordenados. En otras palabras, podemos definir una relación como un conjunto de pares ordenados.
Tipos de funciones
Las funciones se pueden clasificar en términos de relaciones de la siguiente manera:
- Función inyectiva o unívoca: La función inyectiva f: P → Q implica que hay un elemento distinto de Q por cada elemento de P.
- De muchos a uno: La función muchos a uno mapea dos o más elementos de P al mismo elemento del conjunto Q.
- La función suryectiva o onto: Es una función para la que cada elemento del conjunto Q tiene una preimagen en el conjunto P
- La función biyectiva.
Las funciones comunes en el álgebra son:
- Función lineal
- Funciones inversas
- Función constante
- Función de identidad
- Función de valor absoluto
¿Cómo determinar si una relación es una función?
Podemos comprobar si una relación es una función de forma gráfica o siguiendo los siguientes pasos.
- Examine los valores de x o de entrada.
- Examine también los valores de y o de salida.
- Si todos los valores de entrada son diferentes, entonces la relación se convierte en una función, y si los valores se repiten, la relación no es una función.
Vídeos de Función y relación
Contenido