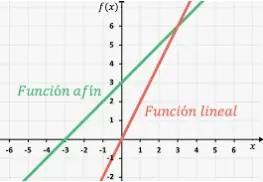
Función afín
Una función es una relación que describe que sólo debe haber una salida para cada entrada (o) podemos decir que un tipo especial de relación (un conjunto de pares ordenados), que sigue una regla, es decir, cada valor X debe estar asociado con un solo valor y se llama función.
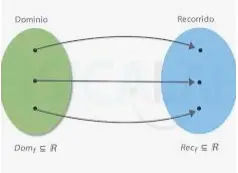
Dominio
Es una colección de los primeros valores del par ordenado (Conjunto de todos los valores de entrada (x)).
Rango
Es una colección de los segundos valores del par ordenado (Conjunto de todos los valores de salida (y)).
Ejemplo:
En la relación, {(-2, 3), {4, 5), (6, -5), (-2, 3)},
El dominio es {-2, 4, 6} y el rango es {-5, 3, 5}.
Nota: No consideres los duplicados al escribir el dominio y el rango y también escríbelo en orden creciente.
Tipos de funciones
En términos de relaciones, podemos definir los tipos de funciones como:
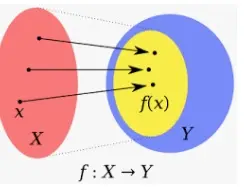
- Función uno a uno o Función inyectiva: Una función f: P → Q se dice que es uno a uno si para cada elemento de P existe un elemento distinto de Q.
- Función de muchos a uno: Una función que mapea dos o más elementos de P al mismo elemento del conjunto Q.
- Función onto o función suryectiva: Una función para la que todo elemento del conjunto Q tiene una preimagen en el conjunto P
- Correspondencia uno-uno o Función biyectiva: La función f coincide con cada elemento de P con un elemento discreto de Q y cada elemento de Q tiene una preimagen en P.
Funciones especiales en álgebra
Algunas de las funciones importantes son las siguientes:
- Función Constante
- Función de identidad
- Función lineal
- Función de Valor Absoluto
- Funciones inversas
¿Qué es la Relación?
Es un subconjunto del producto cartesiano. O simplemente, un conjunto de puntos (pares ordenados). En otras palabras, la relación entre los dos conjuntos se define como la colección del par ordenado, en la que el par ordenado está formado por el objeto de cada conjunto.
Ejemplo: {(-2, 1), (4, 3), (7, -3)}, normalmente escrito en forma de notación de conjuntos con corchetes.
Representación de relaciones
También hay otras formas de escribir la relación, aparte de la notación de conjuntos, como por ejemplo mediante tablas, representándola en el eje XY o mediante un diagrama de mapeo.
Tipos de relaciones
Los diferentes tipos de relaciones son los siguientes:
- Relaciones vacías
- Relaciones universales
- Relaciones de identidad
- Relaciones inversas
- Relaciones reflexivas
- Relaciones simétricas
- Relaciones transitivas
- Relación vacía
Cuando no hay ningún elemento del conjunto X que esté relacionado o mapeado con algún elemento de X, entonces la relación R en A es una relación vacía, y también llamada relación nula, es decir, R= ∅.
Por ejemplo, si hay 100 mangos en la cesta de la fruta. No hay posibilidad de encontrar una relación R de conseguir alguna manzana en la cesta. Por lo tanto, R es Nula ya que tiene 100 mangos y ninguna manzana.
Relación universal
R es una relación en un conjunto, digamos A es una relación universal porque, en esta relación completa, cada elemento de A está relacionado con cada elemento de A. es decir R = A × A.
Es una relación completa ya que cada elemento del conjunto A está en el conjunto B.
Relación de identidad
Si cada elemento del conjunto A está relacionado sólo consigo mismo, se llama relación de identidad.
I={(A, A), ∈ a}.
Por ejemplo,
Cuando lanzamos un dado, el número total de resultados posibles es 36. Es decir, (1, 1) (1, 2), (1, 3)…..(6, 6). Si consideramos la relación (1, 1), (2, 2), (3, 3) (4, 4) (5, 5) (6, 6), es una relación de identidad.
Relación inversa
Si R es una relación del conjunto A al conjunto B, es decir, R ∈ A X B. La relación R – 1 = {(b,a):(a,b) ∈ R}.
Por ejemplo,
Si se lanzan dos dados si R = {(1, 2) (2, 3)}, R – 1 = {(2, 1) (3, 2)}. Aquí el dominio es el rango R – 1 y viceversa.
Relación reflexiva
Una relación es una relación reflexiva si cada elemento del conjunto A se asigna a sí mismo, es decir, para cada a ∈ A, (a, a) ∈ R.
Relación simétrica
Una relación simétrica es una relación R sobre un conjunto A si (a, b) ∈ R entonces (b, a) ∈ R, para todo a y b ∈ A.
Relación transitiva
Si (a, b) ∈ R, (b, c) ∈ R, entonces (a, c) ∈ R, para todo a,b,c ∈ A y esta relación en el conjunto A es transitiva.
Relación de equivalencia
Si una relación es reflexiva, simétrica y transitiva, entonces la relación se llama relación de equivalencia.
Vídeos de Función afín

Contenido