Cosec

Cosec

La cosecante es el recíproco del seno. Tenemos seis funciones trigonométricas importantes:

• Seno
• Coseno
• Tangente
• Cotangente
• Secante
• Cosecante

Como es el recíproco de sen x, se define como el cociente entre la longitud de la hipotenusa y la longitud de la perpendicular de un triángulo rectángulo.

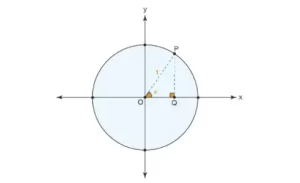
Considera una circunferencia unitaria con los puntos O como centro, P en la circunferencia y Q dentro de la circunferencia y únelos como se muestra arriba. Como se trata de una circunferencia unitaria, la longitud de OP es igual a la unidad. Consideremos que la medida del ángulo POQ es igual a x grados. Entonces, utilizando la definición de cosecante, tenemos

csc x = OP/PQ

= 1/PQ

Fórmula de la función cosecante

Como la función cosecante es la recíproca de la función seno, podemos escribir su fórmula como

Cosec x = 1 / sin x

Además, como la fórmula de sen x se escribe como

Sin x = Perpendicular / Hipotenusa y csc x es el recíproco de sin x, podemos escribir la fórmula de la función cosecante como

Cosec x = Hipotenusa / Perpendicular

Dominio y rango de la cosecante x

Como hemos comentado antes, la cosecante es el recíproco de la función seno, es decir, csc x = 1 / sin x, el cosec x está definido para todos los números reales excepto para los valores en los que sin x es igual a cero. Sabemos que sin x es igual a para todos los múltiplos integrales de pi, es decir, que sin x = 0 implica que ese x = nπ, donde n es un número entero. Por tanto, cosec x está definido para todos los números reales excepto nπ. Ahora, sabemos que el rango de sen x es [-1, 1] y csc x es el recíproco de sen x, por lo que el rango de csc x son todos los números reales excepto (-1, 1). Así que el dominio y el rango de la cosecante están dados por

Dominio = R – nπ
Rango = (-∞, -1] U [+1, +∞)

Gráfica de la cosecante

Ahora que conocemos el dominio y el rango de la cosecante, vamos a trazar su gráfica. Como sabemos la cosecante x está definida para todos los números reales excepto para los valores en los que sen x es igual a cero. Por tanto, tenemos asíntotas verticales en los puntos en los que csc x no está definida. Además, utilizando los valores de sen x, tenemos y = csc x como

Cuando x = 0, sin x = 0 y por lo tanto, csc x = no está definido
Cuando x = π/6, sin x = ½, csc x = 2
Cuando x = π/4, sin x = 1/√2, csc x = √2
Cuando x = π/3, sin x = √3/2, csc x = 2/√3
Cuando x = π/2, sin x = 1, csc x = 1

Vídeos de Cosec