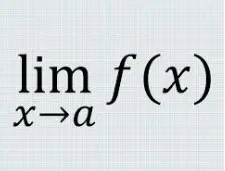Cálculo de límites

por
Cálculo de límites
Los ejemplos de límites son uno de los conceptos más difíciles en Matemáticas según muchos estudiantes. Sin embargo, a través de una comprensión más fácil y una práctica continuada, los estudiantes pueden llegar a conocer a fondo los conceptos de qué son los límites en matemáticas, el límite de una función ejemplo, la definición de límites y las propiedades de los límites. La matemática de los límites es uno de los conceptos más importantes del Cálculo. El cálculo es una rama de las matemáticas que se ocupa de los cálculos relacionados con cantidades que cambian continuamente. La fórmula del límite matemático puede definirse como el valor que una función devuelve como salida para los valores de entrada dados.

Cálculo de límites

La matemática de límites es muy importante en el cálculo. Es uno de los prerrequisitos básicos para entender otros conceptos del Cálculo como la continuidad, la diferenciación, la fórmula de límite de integración, etc. La mayoría de las veces, las fórmulas matemáticas de límites son la representación del comportamiento de la función en un punto concreto. De ahí que se utilice el concepto de límite para analizar la función. El concepto matemático de Límite de una red topológica generaliza el límite de una secuencia y, por tanto, relaciona las matemáticas de límites con la categoría de teoría. Las integrales en general se clasifican en integrales definidas e indefinidas.

En el caso de la fórmula de límite de integración definida se especifican los límites superior e inferior. Sin embargo, las fórmulas límite de integración indefinidas se definen sin límites especificados y, por tanto, tienen una constante arbitraria después de la integración. Las secciones subsiguientes elaboran un breve resumen de varios conceptos involucrados en una mejor comprensión de la fórmula matemática de límite.Fórmula de límite:- Sea y = f(x) como una función de x. Si en un punto x = a, f(x) toma forma indeterminada, entonces podemos considerar los valores de la función que está muy cerca de a. Si estos valores tienden a algún número único definido como x tiende a a, entonces ese número único obtenido se llama el límite de f(x) en x = a.

Obtuvimos

limx→ac=c
limx→ax=a

Si los límites existen, se obtiene con los límites correspondientes u,v

  • limx→af(x)±g(x)=u±v
  • limx→acg(x)=cv
  • limx→af(x)g(x)=uv
  • limx→af(x)g(x)=uv si v≠0

Si los límites existen y si f(x) es continua

  • limx→af(x)=f(a)
  • limx→af(x)±g(x)=f(a)±g(a)
  • limx→acf(x)=cf(a)
  • limx→af(x)g(x)=f(a)g(a)
  • limx→af(x)g(x)=f(a)g(a) si g(a)≠0
  • Si f es continua y existe limx→ag(x) y si f(x) está definida en limx→ag(x)
  • limx→af(g(x))=f(limx→ag(x))

Como reglas tenemos:

  • ∀x en un intervalo abierto, que contiene a:
  • u(x)≤v(x)≤w(x)⟹limx→au(x)≤limx→av(x)≤limx→aw(x)
  • si f(x) y g(x) son diferenciables y si limx→af(x),g(x)=±∞ o limx→af(x),g(x)=0 y si existe limx→af′(x)g′(x)
  • limx→af(x)g(x)=limx→af′(x)g′(x)

Vídeos de Cálculo de límites

https://www.youtube.com/watch?v=hkyM-WjLNFQ

Contenido