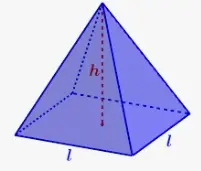
Area lateral de una piramide
Al igual que otras formas tridimensionales, una pirámide cuadrada también tiene dos tipos de áreas.
- Superficie lateral (LSA)
- Área superficial total (AST)
Conozcamos el área lateral de una pirámide cuadrada junto con la fórmula y algunos ejemplos resueltos aquí. Al final puedes encontrar algunas preguntas de práctica.
¿Qué es el área lateral de una pirámide cuadrada?
La palabra «lateral» significa «perteneciente al lado». Así que el área lateral de una pirámide cuadrada es la suma de las áreas de sus caras laterales. Esto también se conoce como el área de la superficie lateral (LSA) de la pirámide cuadrada. Sabemos que una pirámide cuadrada tiene
- una base que es un cuadrado.
- 4 caras laterales, cada una de las cuales es un triángulo.
Todos estos triángulos son congruentes e isósceles y cada uno de ellos tiene un lado que coincide con un lado de la base (cuadrado).
Así, la superficie lateral de una pirámide cuadrada es la suma de las áreas de cuatro de sus caras laterales triangulares.
Fórmula del área lateral de una pirámide cuadrada
Consideremos una pirámide cuadrada cuya longitud de la base (longitud de los lados del cuadrado) es «a» y la altura de cada cara lateral (triángulo) es «l» (también se conoce como altura de la inclinación), es decir, la base y la altura de cada una de las 4 caras triangulares son «a» y «l» respectivamente. Por tanto, el área de cada una de esas caras triangulares es 1/2 × a × l. Así que la suma de las áreas de las 4 caras triangulares es, 4 ( ½ al) = 2 al. Por tanto, el área lateral de una pirámide cuadrada = 2al
¿Y si nos dan la altura de la pirámide en lugar de dar la altura de la inclinación? Supongamos que la altura de la pirámide (altitud) es «h». Entonces, aplicando el teorema de Pitágoras (puedes consultar la siguiente figura)
l=√[(a2/4) + h2]
Sustituyendo esto en la fórmula anterior,
El área lateral de una pirámide cuadrada = 2al = 2a√[(a2/4) + h2
¿Cómo calcular el área lateral de una pirámide cuadrada?
La superficie de una pirámide lateral se puede calcular siguiendo los pasos dados,
- Observa las dimensiones dadas de la pirámide cuadrada y comprueba que deben tener las mismas unidades.
- Aplica la fórmula para calcular el área lateral de la pirámide cuadrada,
- Área lateral de una pirámide cuadrada = 2al = 2a√[(a2/4) + h2], donde, ‘a’ es la longitud de la base, ‘h’ es la altura y ‘l’ es la altura oblicua de la pirámide cuadrada.
- Expresa la respuesta con unidades cuadradas.
Vídeos de Area lateral de una piramide
Contenido