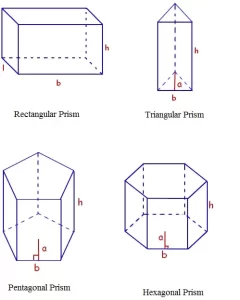
Area de un prisma
Un prisma es un poliedro que tiene dos bases paralelas congruentes unidas lateralmente por caras de paralelogramo o rectangulares (en el caso de los prismas rectos). El número de superficies laterales es igual al número de lados del polígono base. Para un polígono base de n lados, el prisma tendrá n caras rectangulares. Por tanto, el número total de superficies de un prisma con una base poligonal de n lados es n+2n+2n + 2. Consideremos un prisma de este tipo cuya longitud es h y cuya longitud lateral y apotema de su base son respectivamente b y a. En general, la superficie lateral de un prisma es igual al producto de la longitud del prisma por el perímetro de su base.
Un prisma es un poliedro con 2 bases poligonales paralelas entre sí. Las dos bases poligonales están unidas por caras laterales. El número de caras laterales es igual al número de lados de la base. Las caras laterales de un prisma son perpendiculares a las bases poligonales. La superficie de un prisma es la suma del área de las 2 bases poligonales y el área de las caras laterales. La superficie de un prisma se mide en términos de unidades cuadradas.
Tipos de prisma
La fórmula de la superficie de un prisma es la siguiente
El área de un prisma rectangular es A = 2 (wl + lh + hw)
La superficie de un prisma triangular es A = bh + L (s1 + s2 + s3)
Fórmula de la superficie de un prisma pentagonal
Donde
a – longitud apotema del prisma.
b – longitud de la base del prisma.
l – ancho de la base del prisma rectangular.
h – altura del prisma.
La fórmula de la superficie de un prisma es la siguiente
El área de la superficie de un prisma rectangular es A = 2 (wl + lh + hw)
La superficie de un prisma triangular es A = bh + L (s1 + s2 + s3)
Problemas de la superficie de un prisma
A continuación se presentan algunos problemas resueltos sobre el área de la superficie de un prisma:
- ¿Cuál será la superficie de un prisma triangular si la longitud de la apotema, la longitud de la base y la altura son 7 cm, 10 cm y 18 cm respectivamente?
Solución:
Dada,
a = 7 cm
b = 10 cm
h = 18 cm
Superficie de un prisma triangular
= ab + 3bh
= (7 cm 10 cm) + (3 10 cm 18 cm)
= 70 cm2 + 540 cm2
= 610 cm2
- Calcula la superficie de un prisma pentagonal cuya longitud de la apotema, la longitud de la base y la altura son 12 cm, 15 cm y 21 cm respectivamente?
Solución:
Dada,
a = 12 cm
b = 15 cm
h = 21 cm
Superficie de un prisma pentagonal
= 5ab + 5bh
= (5 12 cm 15 cm) + (5 15 cm 21 cm)
= 900 cm2 + 1575 cm2
= 2475 cm2
Vídeos de Area de un prisma
Contenido