Funcion concava
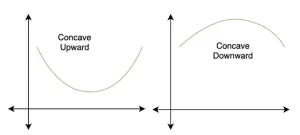
Por ejemplo, si la función se abre hacia arriba se llama cóncava hacia arriba y si se abre hacia abajo se llama cóncava hacia abajo. La figura siguiente muestra dos funciones que son cóncavas hacia arriba y cóncavas hacia abajo respectivamente.
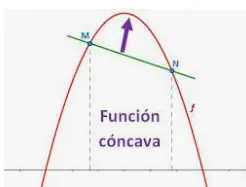
La concavidad también se puede identificar dibujando tangentes en puntos de la gráfica. Por ejemplo, se dice que una gráfica es cóncava hacia arriba en un punto si una tangente trazada a la gráfica en ese punto se encuentra por debajo de la gráfica en las proximidades de ese punto. Del mismo modo, se dice que la gráfica es cóncava hacia abajo en un punto si una tangente dibujada a la gráfica en ese punto se encuentra por encima de la gráfica en la vecindad de ese punto. Esto se puede ver en la figura que se da a continuación,
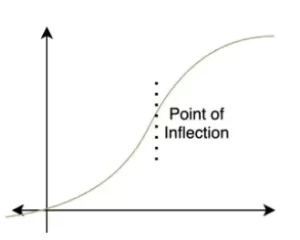
Obsérvese que también puede haber un punto en el que la tangente trazada a él no esté ni por encima ni por debajo de la gráfica. Dichas tangentes intersecan la gráfica en ese punto. En ese punto, la concavidad cambia de arriba a abajo o viceversa. Este punto se llama punto de inflexión.
Veamos ahora la definición formal de todos estos puntos,
Digamos que tenemos una función f(x),
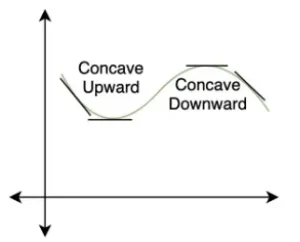
- Se dice que f(x) es cóncava hacia arriba en el intervalo I si todas las posibles tangentes trazadas a la curva en diferentes puntos del intervalo I, se encuentran por debajo de la gráfica.
- Se dice que f(x) es cóncava hacia abajo en el intervalo I si todas las posibles tangentes dibujadas a la curva en diferentes puntos del intervalo I, se encuentran por encima de la gráfica.
- Un punto x = a en la curva f(x) se llama punto de inflexión si la función es continua y la concavidad de la gráfica cambia en ese punto.
Análisis del estado de las funciones cóncavas (concavidad) mediante las derivadas
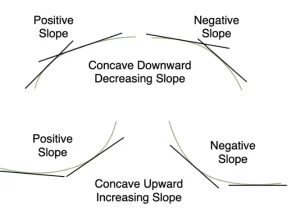
El método anterior es un método gráfico para analizar la concavidad de la función, pero a veces no tenemos la gráfica de la función. Cuando no tenemos conocimiento de la gráfica de la función, las derivadas vienen a nuestro rescate. Supongamos que tenemos una función f(x). Consideremos los diferentes casos dados en la figura siguiente, sabemos que la pendiente de la tangente nos da el valor de la derivada de la función en ese punto de contacto.
Observa que en la figura anterior, cuando la función es cóncava hacia abajo, la pendiente de la tangente tiene un valor decreciente que significa que las derivadas son decrecientes. Del mismo modo, cuando la función es cóncava hacia arriba el valor de las derivadas es decreciente. Por lo tanto, podemos sacar las siguientes conclusiones:
- Si la función es cóncava hacia arriba, su derivada f'(x) es decreciente.
- Si la función es cóncava hacia abajo, su derivada f'(x) es creciente.
- Cuando la función f(x) tiene un punto de inflexión en el punto x = a. f'(x) pasa de ser creciente a decreciente o viceversa.
- Esto significa que la gráfica de la función f'(x) tiene un mínimo/máximo en x = a.
- Podemos extraer reglas matemáticas de estas observaciones dadas anteriormente,
Digamos que tenemos una función f(x),
- Para el intervalo I, si f»(x) > 0 entonces la función f(x) es cóncava hacia arriba en el intervalo I.
- Para el intervalo I, si f»(x) < 0 entonces la función f(x) es cóncava hacia abajo en el intervalo I.
- Si x = a es un punto de inflexión, entonces en x = a, f»(a) = 0.
Vídeos de Funcion concava
Contenido