Volumen de un tronco de piramide
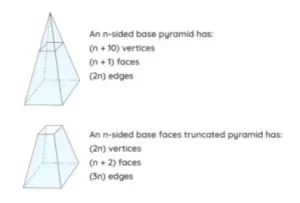
El volumen de una pirámide truncada es el número de unidades cúbicas que puede contener una pirámide truncada. Una pirámide tiene un vértice y una sola cara en la base, mientras que una pirámide truncada no tiene vértice y tiene dos caras en la base, una en la parte superior y otra en la inferior. Sólo la base de una pirámide es un polígono, el resto de las caras son triángulos. Una pirámide puede ser «recta», en la que su vértice está directamente sobre el centroide de su base, o bien una pirámide puede ser «oblicua», que son básicamente pirámides no rectas. Las pirámides reciben el nombre de sus bases, por ejemplo, una pirámide con base triangular se llama base triangular, una pirámide con base cuadrada se llama pirámide cuadrada, una pirámide con base octogonal se llama pirámide octogonal, etc. Una pirámide con una base de ‘n’ lados tiene ‘n+1’ vértices, ‘n+1’ caras y ‘2n’ aristas. En el caso de una pirámide truncada, las dos caras de la base deben tener lados iguales, por lo que una pirámide truncada con caras de la base de ‘n’ lados tiene ‘2n’ vértices, ‘n+2’ caras y ‘3n’ aristas. Por ejemplo, se puede expresar como m3, cm3, in3, etc. dependiendo de las unidades dadas.
Fórmula del volumen de una pirámide truncada
Como sabemos que una pirámide truncada se forma cortando una pirámide a lo largo de su sección transversal, este concepto nos ayudará a entender la fórmula del volumen de una pirámide truncada.
Por tanto, el volumen de una pirámide truncada = Volumen de la pirámide entera – Volumen de la pirámide pequeña.
Volumen de una pirámide truncada
Así, la fórmula del volumen de una pirámide truncada es V = 1/3 × h × (a2 + b2 + ab) donde «V», «h», «a» y «b» son el volumen de la pirámide truncada, la altura de la pirámide truncada, la longitud lateral de la base de la pirámide entera y la longitud lateral de la base de la pirámide pequeña.
Consideremos que la base de la pirámide entera es un cuadrado de lado «a» unidades y la base de la pirámide pequeña en la parte superior es un cuadrado de lado «b» unidades. Además, consideremos que la altura de la pirámide entera es «H» unidades, la altura de la pirámide truncada será «h» unidades, por lo tanto, la altura de la pirámide pequeña será «H-h» unidades.
Volumen de una pirámide truncada, V = Volumen de la pirámide entera – Volumen de la pirámide pequeña.
⇒ V = (1/3 × Área de la base de la pirámide entera × Altura de la pirámide entera) – (1/3 × Área de la base de la pirámide pequeña × Altura de la pirámide pequeña)
⇒ V = (1/3 × a2 × H) – (1/3 × b2 × (H – h)
⇒ V = 1/3 × (a2H – b2(H – h))
⇒ V = 1/3 × (a2H – b2H + b2h)
⇒ V = 1/3 × ((a2 – b2)H + b2h) …(1)
Ahora, la relación entre las alturas de la pirámide entera y la pirámide pequeña, H:(H – h) = a:b. Por lo tanto, la relación entre la pirámide entera y la pirámide truncada sería, H: h = a:(a – b)
⇒ H/h = a/(a – b)
⇒ H = (a/(a – b)) × h …(2)
Sustituyendo el valor de «H» de la ecuación (2) en la ecuación (1), obtenemos:
⇒ V = 1/3 × ((a2 – b2)(a/(a – b)) × h) + b2h))
⇒ V = 1/3 × (((a + b)(a – b) × a)/(a – b)) × h + b2h
⇒ V = 1/3 × (a + b) × a × h + b2h
⇒ V = 1/3 × h × (a2 + b2 + ab)
Así, el volumen de una pirámide truncada viene dado por, V = 1/3 × h × (a2 + b2 + ab).
¿Cómo encontrar el volumen de una pirámide truncada?
Podemos encontrar el volumen de una pirámide truncada siguiendo los siguientes pasos:
Paso 1: Identificar las dimensiones dadas como la altura de la pirámide truncada, la longitud lateral de la base de la pirámide entera y la longitud lateral de la pirámide más pequeña.
Paso 2: Sustituye los valores en la fórmula V = 1/3 × h × (a2 + b2 + ab) para determinar el valor del volumen de una pirámide truncada.
Paso 3: Escribe la respuesta obtenida con unidades cúbicas.
Vídeos de Volumen de un tronco de piramide
Contenido