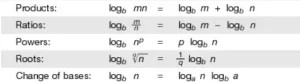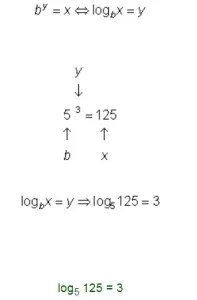Funcion logaritmica
Los científicos adoptaron rápidamente los logaritmos debido a varias propiedades útiles que simplificaban los cálculos largos y tediosos. En particular, los científicos podían encontrar el producto de dos números m y n buscando el logaritmo de cada número en una tabla especial, sumando los logaritmos y consultando de nuevo la tabla para encontrar el número con ese logaritmo calculado (conocido como su antilogaritmo). Expresada en términos de logaritmos comunes, esta relación viene dada por log mn = log m + log n. Por ejemplo, 100 × 1.000 puede calcularse buscando los logaritmos de 100 (2) y 1.000 (3), sumando los logaritmos (5) y encontrando luego su antilogaritmo (100.000) en la tabla. Del mismo modo, los problemas de división se convierten en problemas de resta con logaritmos: log m/n = log m – log n. Esto no es todo; el cálculo de potencias y raíces puede simplificarse con el uso de logaritmos. Los logaritmos también se pueden convertir entre cualquier base positiva (excepto que el 1 no se puede utilizar como base ya que todas sus potencias son iguales a 1).
Definición de Logaritmo
El logaritmo de x en base b se escribe logb x y se define como
logb x = y si y sólo si by = x, donde x > 0 y b > 0, b ≠ 1.
Ejemplo de función logaritmica
Reescribe 5^3 = 125 como una ecuación logarítmica.
Tienes que reescribirla en la forma logb x = y.
Aquí la base es 5 y el exponente es 3.
Sustituye b, y y x en la ecuación logarítmica,
Vídeos de Funcion logaritmica
Contenido