Razones trigonométricas
Relaciones trigonométricas
- Sin θ Lado opuesto a θ/Hipotenusa
- Cos θ Lado adyacente a θ/Hipotenusa
- Tan θ Lado opuesto/lado adyacente y Sin θ/Cos θ
- Cot θ Lado adyacente/Lado opuesto y 1/tan θ
- Sec θ Hipotenusa/Lado adyacente & 1/cos θ
- Cosec θ Hipotenusa/Lado opuesto & 1/sin θ
Las razones trigonométricas se definen como los valores de todas las funciones trigonométricas basadas en el valor de la razón de los lados de un triángulo rectángulo. Las razones de los lados de un triángulo rectángulo con respecto a cualquiera de sus ángulos agudos se conocen como razones trigonométricas de ese ángulo en particular.
Los tres lados del triángulo rectángulo son:
- Hipotenusa (el lado más largo)
- Perpendicular (lado opuesto al ángulo)
- Base (lado adyacente al ángulo)
¿Cómo encontrar las razones trigonométricas?
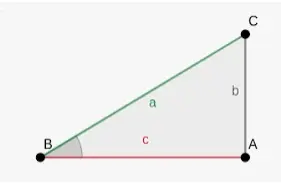
Consideremos un triángulo rectángulo, con ángulo recto en B.
Con respecto a ∠C, las razones trigonométricas se dan como
- seno: El seno de un ángulo se define como la relación entre el lado opuesto(lado perpendicular) a ese ángulo y la hipotenusa.
- coseno: El coseno de un ángulo se define como la relación entre el lado adyacente a ese ángulo y la hipotenusa.
- tangente: La tangente de un ángulo se define como la relación entre el lado opuesto a ese ángulo y el lado adyacente a ese ángulo.
- cosecante: La cosecante es la inversa multiplicativa del seno.
- secante: La secante es la inversa multiplicativa del coseno.
- cotangente: La cotangente es la inversa multiplicativa de la tangente.
Las relaciones anteriores se abrevian como sin, cos, tan, cosec, sec y tan respectivamente en el orden en que se describen. Así, para Δ ABC, los cocientes se definen como
- sin C = (Lado opuesto a ∠C)/(Hipotenusa) = AB/AC
- cos C = (Lado adyacente a ∠C)/(Hipotenusa) = BC/AC
- tan C = (Lado opuesto a ∠C)/(Lado adyacente a ∠C) = AB/BC = sin ∠C/cos ∠C
- cosec C= 1/sin C = (Hipotenusa)/ (Lado opuesto a ∠C) = AC/AB
- sec C = 1/cos C = (Hipotenusa)/ (Lado opuesto a ∠C) = AC/BC
- cot C = 1/tan C = (Lado adyacente a ∠C)/(Lado opuesto a ∠C)= BC/AB
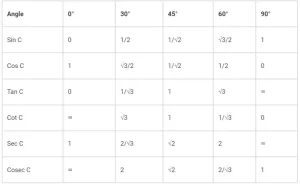
En Δ ABC, si ∠A y ∠C se asumen como 30° y 60°, entonces puede haber infinitos triángulos rectos con esas especificaciones pero todas las razones escritas arriba para ∠C en todos esos triángulos serán iguales. Por lo tanto, todos los cocientes para cualquiera de los ángulos agudos (ya sea ∠A o ∠C) serán los mismos para cada triángulo rectángulo. Esto significa que los cocientes son independientes de las longitudes de los lados del triángulo.
Aplicaciones de la trigonometría
La trigonometría es una de las ramas más importantes de las matemáticas. Algunas de las aplicaciones de la trigonometría son
- Medir la altura de torres o grandes montañas
- Determinar la distancia de la costa al mar
- Encontrar la distancia entre dos cuerpos celestes
- Determinar la potencia de los paneles de células solares con diferentes inclinaciones
- Representar diferentes magnitudes físicas como ondas mecánicas, ondas electromagnéticas, etc.
- De los ejemplos anteriores se desprende que la trigonometría interviene en una parte importante de nuestra vida cotidiana y mucho más. En la mayoría de las aplicaciones enumeradas anteriormente, se estaba midiendo algo y de eso trata la trigonometría.
Vídeos de Razones trigonométricas
Contenido