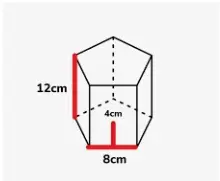
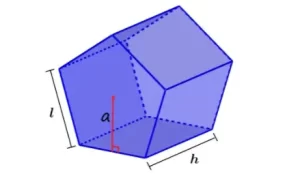
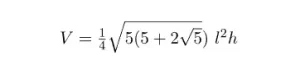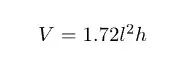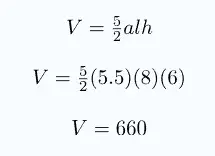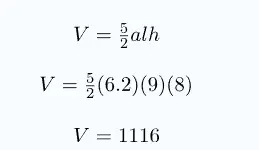Volumen de un prisma pentagonal
Podemos encontrar el volumen de un prisma pentagonal multiplicando el área de la base por la altura del prisma. Recordemos que podemos utilizar la apotema para calcular fácilmente el área de los polígonos. Por tanto, tenemos la siguiente fórmula
donde a representa la longitud de la apotema, l representa la longitud de los lados de la base pentagonal y h representa la longitud de la altura del prisma.
Además, también podemos encontrar el volumen de un prisma utilizando únicamente la longitud de su altura y la longitud de uno de los lados de su base hexagonal. Para ello, utilizamos la siguiente fórmula:
Esta fórmula es más complicada, pero podemos aproximarla a la siguiente expresión:
Ejemplos de Volumen de un prisma pentagonal
- ¿Cuál es el volumen de un prisma que tiene una altura de 6 m y una base con lados de 8 m de longitud y una apotema de 5,5 m?
Solución
Tenemos la siguiente información:
Altura del prisma, h=6
Lados del pentágono, l=8
Apotema, a=5,5
Utilizando la primera fórmula del volumen con esta información, tenemos:
El volumen del prisma es de 660 m³.
- Un prisma tiene una altura de 8 m y su base es un pentágono con lados de 9 m de longitud y una apotema de 6,2 m. ¿Cuál es su volumen?
Solución
Reconocemos los siguientes valores:
Altura del prisma, h=8
Lados del pentágono, l=9
Apotema, a=6,2
Sustituimos estos valores en la primera fórmula del volumen:
El volumen del prisma es 1116 m³.
Vídeos de Volumen de un prisma pentagonal
https://www.youtube.com/watch?v=Ajm-yXfAxLc
Contenido