Tetraedro
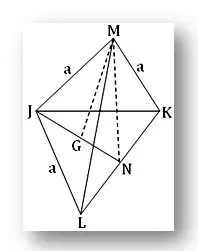
En la figura dada se ha representado un tetraedro regular. M es el vértice y el triángulo equilátero JLK es la base del tetraedro regular. JL, LK, KJ, MJ, ML y MK son sus seis aristas y tres caras laterales son triángulos equiláteros congruentes LKM, KJM y JLM. Si G es el centroide de la base JLK y N, el punto medio del lado LK entonces MG es la altura y MN, la altura oblicua del tetraedro regular.
Sea a la longitud de una arista de un tetraedro regular. Entonces,
Área de la superficie inclinada del tetraedro regular
= suma de las áreas de tres triángulos equiláteros congruentes
= 3 ∙ (√3)/4 a² unidades cuadradas;
Área de toda la superficie del tetraedro regular
= suma de las áreas de cuatro triángulos equiláteros congruentes.
= 4 ∙ (√3)/4 a²
= √3 a² unidades cuadradas;
Volumen del tetraedro regular
= 1/3 × área de la base × altura
= (1/3) ∙ (√3)/4 ∙ a² × (√2)/(√3) a
= (√2/12) a³ unidades cúbicas.
Esta figura geométrica está formada por cuatro triángulos equiláteros, es decir, triángulos regulares. En otras palabras, es un poliedro regular con cuatro caras triangulares iguales. Este poliedro tiene un total de cuatro caras, seis aristas y cuatro vértices (en cada uno de sus vértices se unen tres caras). Tetraedro
En cuanto a la altura, se puede obtener trazando una perpendicular desde el vértice a la cara opuesta de la figura. Su volumen es igual a un tercio del área de la base multiplicado por su altura. Para calcular el área, calcula el área de uno de sus triángulos y multiplícala por cuatro.
También existen los tetraedros irregulares, que están formados por cuatro poliedros diferentes. Hay dos variantes: el trirectángulo y el isofacial. El primero tiene tres caras formadas por triángulos rectos y sus alturas coinciden en el mismo punto. El segundo está formado por tres triángulos isósceles iguales.
Vídeos de Tetraedro
Contenido