¿Qué es la excentricidad y cómo se determina?
La excentricidad de una elipse mide el grado de achatamiento de un círculo. Es igual a la raíz cuadrada de [1 – b*b/(a*a)]. La letra a representa el semieje mayor, ½ de la distancia a través del eje largo de la elipse. La letra b representa el semieje mayor, ½ de la distancia a través del eje corto de la elipse. Para un círculo perfecto, a y b son iguales, de modo que la excentricidad es cero. La órbita de la Tierra tiene una excentricidad de 0,0167, por lo que es casi un círculo perfecto.
Tercera ley de kepler fórmula
El tiempo que tarda un planeta en dar la vuelta al Sol (su periodo, P) está relacionado con la distancia media del planeta al Sol (d). Es decir, el cuadrado del período, P*P, dividido por el cubo de la distancia media, d*d*d, es igual a una constante. Para cada planeta, independientemente de su período o distancia, P*P/(d*d*d) es el mismo número.
La Tercera Ley de Kepler es el último de los teoremas revolucionarios del astrónomo alemán Johannes Kepler y explica las órbitas planetarias alrededor del sol.
Antes de que Kepler esbozara sus leyes del movimiento planetario a principios del siglo XVII, el conocimiento de la humanidad sobre el sistema solar y más allá estaba en su infancia y seguía siendo en gran medida un misterio. En la época de Kepler se pensaba que la Tierra era el centro del sistema solar, y quizás del propio universo.
Incluso los modelos heliocéntricos más precisos del sistema solar, que situaban al Sol en su centro, eran incompletos y sugerían que los planetas se movían en círculos ordenados alrededor de sus estrellas.
Las leyes de Kepler desplazarían ligeramente la estrella del centro de este modelo a un punto focal, aplanando las órbitas de los planetas, y sugieren que estos cuerpos planetarios se mueven a velocidades que varían en función de la proximidad a su estrella.
Propiedades de las elipses leyes uno y dos
Una de las claves para entender las leyes de Kepler sobre el movimiento planetario reside en las propiedades de las elipses.
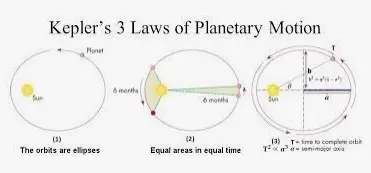
La primera propiedad de las elipses es que están definidas por dos focos, los focos. La suma de las distancias a cualquier punto de una elipse es siempre una constante. En el caso de las órbitas planetarias, esto conduce a la primera ley de Kepler: «la órbita de un planeta es una elipse con el Sol en uno de los dos focos».
Esto significa que el planeta y su estrella orbitan alrededor de un centro de masa mutuo, pero como la masa de la estrella es mucho mayor que la de su planeta, ese centro de masa no sólo está más cerca de la estrella, sino que a menudo está debajo de su superficie.
La segunda propiedad de una elipse define la diferencia entre esta forma y un círculo. Una elipse es un círculo aplanado, esta «planitud» se define como excentricidad y toma un valor entre 0 y 1. Así, un círculo perfecto puede considerarse una elipse con una excentricidad de 0. Una parábola sería una elipse con una excentricidad de 1.
Para la segunda ley de Kepler, imaginemos un planeta en una órbita elíptica con una línea que lo une a su estrella madre. A medida que el planeta se mueve, la línea barre un área que es la misma en todo momento.
Sin embargo, debido a la excentricidad, cuando un planeta está más cerca de su estrella la línea que los une es más corta. Esto significa que el área que traza es menos profunda. Así, para trazar la misma zona en el mismo tiempo, el planeta debe moverse más rápidamente.
Así pues, la segunda ley de Kepler nos dice que cuando un planeta está más cerca de su estrella -un punto llamado perihelio- se mueve más rápido. En cambio, cuando el planeta está más alejado de su estrella, en el afelio, se mueve más lentamente.
Es natural agrupar estas dos leyes, ya que nacieron de las observaciones de Brahe, estrechamente guardadas, y se publicaron juntas en la obra de 1609 Astronomia nova (Nueva Astronomía).
La tercera ley de Kepler, también conocida como Ley de la Armonía, tardaría otros diez años en formularse. Publicada en 1619, revelaría la mecánica del sistema solar con un detalle sin precedentes.
«El cuadrado del período orbital de un planeta es proporcional al cubo del semieje mayor de su órbita».
Esa es la Tercera Ley de Kepler en pocas palabras, y surge de la tercera propiedad física de las elipses, relacionada con sus distintos puntos de eje. El eje más largo de la elipse se llama eje mayor, mientras que el más corto se llama eje menor. La mitad del eje mayor se denomina semieje mayor.
La ecuación de la Tercera Ley de Kepler es P² = a³, por lo que el periodo de la órbita de un planeta (P) al cuadrado es igual al tamaño del semieje mayor de la órbita (a) al cubo cuando se expresa en unidades astronómicas.
Lo que la Tercera Ley de Kepler hace en realidad es comparar el período orbital y el radio de la órbita de un planeta con los de otros planetas. Así, a diferencia de la primera y la segunda ley de Kepler, que describen las características del movimiento de un solo planeta, la tercera ley del astrónomo compara el movimiento de diferentes planetas y calcula las armonías de los planetas.
Esta comparación toma la forma de la relación entre los cuadrados de los periodos (T²) y los cubos de sus distancias medias al sol (R³), resultando ser la misma para cada uno de los planetas.
Gracias a esta ley, si conocemos la distancia de un planeta a su estrella, podemos calcular el periodo de su órbita y viceversa. Como la distancia entre la Tierra y el Sol (1 UA) es de unas 92.960.000 millas (149.600.000 kilómetros) y un año terrestre tiene 365 días, se puede calcular la distancia y el periodo orbital de otros planetas cuando sólo se conoce una variable.
En el caso del sistema solar, esto nos da una imagen precisa de la órbita de cada planeta alrededor del sol.
A medida que aumenta la distancia de un planeta al sol, el tiempo que tarda en orbitarlo aumenta rápidamente.
Por ejemplo, Mercurio -el planeta más cercano al sol- completa una órbita cada 88 días. El tercer planeta desde el sol, la Tierra, tarda aproximadamente 365 días en orbitar el sol. Y Saturno, el sexto planeta del sistema solar alejado de su estrella, tarda 10.759. Por supuesto, la Ley Armónica no sólo nos habla de las órbitas de los planetas.
Vídeos de Tercera ley de kepler fórmula
Contenido