Teorema del seno y coseno
Supongamos que, a, b y c son longitudes del lado de un triángulo ABC, entonces;
a2 = b2 + c2 – 2bc cos ∠x
b2 = a2 + c2 – 2ac cos ∠y
c2 = a2 + b2 – 2ab cos ∠z
Ley de los senos, cosenos y tangentes
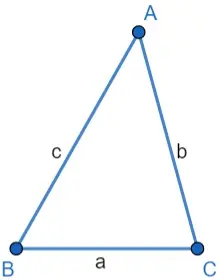
Ley de los senos
El área de un triángulo ABC viene dada por las fórmulas:
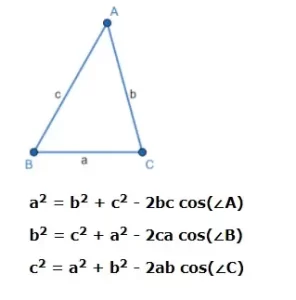
Ley de los cosenos
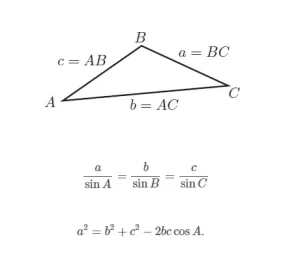
Sean a(la longitud de BC), b(la longitud de CA), c(la longitud de AB) las longitudes de los lados de un triángulo ABC.
Ley de las tangentes
Las reglas del seno y del coseno pueden utilizarse en cualquier triángulo. En el siguiente diagrama, los lados están etiquetados con minúsculas a , b y c y los correspondientes ángulos opuestos a los lados se etiquetan con mayúsculas A , B y C .
Ejemplo del teorema del seno y coseno
En los siguientes ejemplos, a , b y c se refieren a las longitudes de los lados y A , B y C se refieren a los ángulos opuestos correspondientes.
Dado a = 3 , b = 4 , A = 40 ∘ , hallar B
 Vídeos de Teorema del seno y coseno
Vídeos de Teorema del seno y coseno
https://www.youtube.com/watch?v=uanM6Vblmp0
Contenido


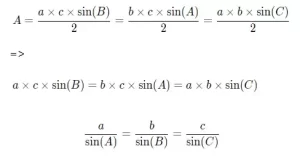
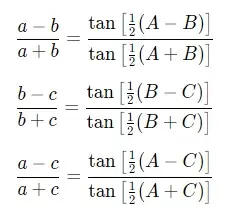
 Vídeos de Teorema del seno y coseno
Vídeos de Teorema del seno y coseno