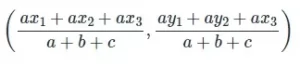Teorema del incentro
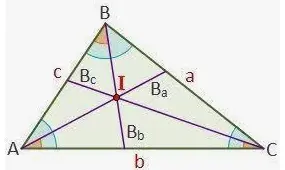
El teorema del incentro establece que el incentro (intersección de la bisectriz del ángulo del triángulo) es equidistante de los tres lados del triángulo.
Este artículo cubre los fundamentos del teorema del incentro y establece las propiedades relacionadas con el incentro y el proceso de localización del incentro en función de los componentes dados del triángulo.
¿Qué es el teorema del incentro?
El teorema del incentro es un teorema que establece que el incentro es equidistante de los lados correspondientes a las bisectrices de los ángulos del triángulo. Las bisectrices de los ángulos del triángulo se cruzan en un punto dentro del triángulo y este punto se llama incentro.
Cómo hallar el incentro de un triángulo
Hay tres maneras de encontrar el incentro del triángulo: utilizando la fórmula algebraica de coordenadas, midiendo el radio interior y construyendo gráficamente el incentro. Cuando se encuentra el incentro de un triángulo, se utiliza el hecho de que los incentros son puntos donde se cruzan las bisectrices de los ángulos.
- Si un triángulo está situado en un sistema de coordenadas, aplique la fórmula del incentro para encontrar las coordenadas del incentro del triángulo.
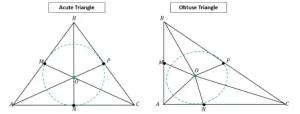
- El incentro también se puede localizar gráficamente construyendo las bisectrices de los ángulos del triángulo.
- Calcula el inradio y construye los inradios de cada uno de los vértices para localizar el incentro del triángulo.
Encontrar el incentro en un plano de coordenadas
Para encontrar el incentro de un triángulo graficado en un plano xy, utiliza las coordenadas de los vértices del triángulo y luego aplica la fórmula del incentro para encontrar la fórmula del incentro.
En geometría, un triángulo es un tipo de polígono bidimensional que tiene tres lados. Cuando los dos lados se unen extremo a extremo, se llama vértice del triángulo. Entre dos lados se forma un ángulo. Es uno de los elementos importantes de la geometría.
Incentro de un triángulo Significado
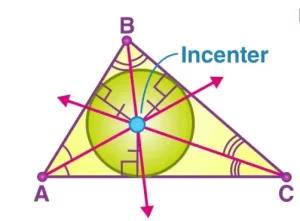
El incentro de un triángulo es el punto de intersección de las tres bisectrices interiores del triángulo. En otras palabras, se puede definir como el punto donde se cruzan las bisectrices de los ángulos interiores del triángulo. Este punto será equidistante de los lados de un triángulo, ya que el punto de unión del eje central es el punto central del círculo inscrito del triángulo.
El incentro de un triángulo es el centro de su círculo inscrito, que es el círculo más grande que cabe dentro del triángulo. Este círculo también se llama círculo inscrito de un triángulo.
Vídeos de Teorema del incentro
Contenido