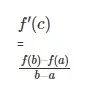Teorema de rolle

por
Teorema de rolle
El teorema de Rolle es un caso particular del teorema del valor medio que satisface ciertas condiciones. A su vez, el teorema del valor medio de Lagrange es el teorema del valor medio propiamente dicho o el primer teorema del valor medio. En general, se puede entender la media como el promedio de los valores dados. Pero en el caso de las integrales, el proceso de encontrar el valor medio de dos funciones diferentes es diferente.

Teorema de rolle

Si una función f está definida en el intervalo cerrado [a,b] satisface las siguientes condiciones

i) La función f es continua en el intervalo cerrado [a, b]

ii)La función f es diferenciable en el intervalo abierto (a, b)

Entonces existe un valor x = c de forma que

f'(c) = [f(b) – f(a)]/(b-a)

Este teorema se conoce también como primer teorema del valor medio o teorema del valor medio de Lagrange.

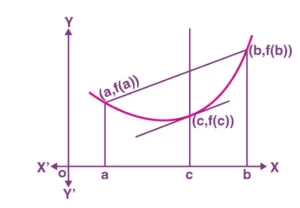
Interpretación geométrica del teorema del valor medio de Lagrange

En la gráfica dada la curva y = f(x) es continua desde x = a y x = b y diferenciable en el intervalo cerrado [a,b] entonces según el teorema del valor medio de Lagrange, para cualquier función que sea continua en [a, b] y diferenciable en (a, b) entonces existe algún c en el intervalo (a, b) tal que la secante que une los puntos extremos del intervalo [a, b] es paralela a la tangente en c.

 

Esto se puede entender mejor con el ejemplo que se da a continuación.

Ejemplo:

Verificar el Teorema del Valor Medio para la función f(x) = x2 – 4x – 3 en el intervalo [a, b], donde a = 1 y b = 4.

Solución:

Dada,

f(x) = x2 – 4x – 3

f'(x) = 2x – 4

a = 1 y b = 4 (dados)

f(a) = f(1) = (1)2 – 4(1) – 3 = 1 – 4 – 3 = -6

f(b) = f(4) = (4)2 – 4(4) – 3 = -3

Ahora,

[f(b) – f(a)]/ (b – a) = (-3 + 6)/(4 – 1) = 3/3 = 1

Según el enunciado del teorema del valor medio, existe un punto c ∈ (1, 4) tal que f'(c) = [f(b) – f(a)]/ (b – a), es decir, f'(c) = 1.

2c – 4 = 1

2c = 5

c = 5/2 ∈ (1, 4)

Verificación: f'(c) = 2(5/2) – 4 = 5 – 4 = 1

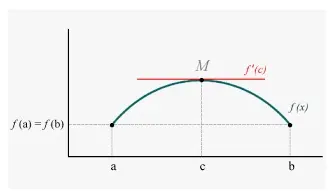
¿Qué es el Teorema de Rolle?

Un caso especial del teorema del valor medio de Lagrange es el Teorema de Rolle que establece que:

Si una función f está definida en el intervalo cerrado [a, b] de forma que satisface las siguientes condiciones.

i) La función f es continua en el intervalo cerrado [a, b]

ii)La función f es diferenciable en el intervalo abierto (a, b)

iii) Ahora bien, si f (a) = f (b) , entonces existe al menos un valor de x, supongamos que este valor es c, que se encuentra entre a y b es decir (a < c < b ) de tal manera que f'(c) = 0 .

Precisamente, si una función es continua en el intervalo cerrado [a, b] y diferenciable en el intervalo abierto (a, b) entonces existe un punto x = c en (a, b) tal que f'(c) = 0

Vídeos de Teorema de rolle

Contenido