Teorema de pitágoras fórmula
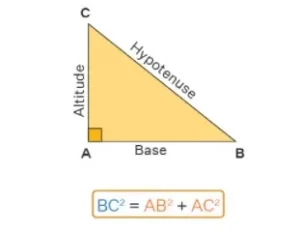
El teorema de Pitágoras establece que si un triángulo es rectángulo (90 grados), el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Observa el siguiente triángulo ABC, en el que tenemos BC2 = AB2 + AC2. Aquí, AB es la base, AC es la altura y BC es la hipotenusa.
Ecuación del Teorema de Pitágoras
La ecuación del teorema de Pitágoras se expresa como, c2 = a2 + b2, donde ‘c’ = hipotenusa del triángulo rectángulo y ‘a’ y ‘b’ son los otros dos catetos. Por lo tanto, cualquier triángulo con un ángulo igual a 90 grados produce un triángulo de Pitágoras y la ecuación de Pitágoras se puede aplicar en el triángulo.
Historia del teorema de Pitágoras
El teorema de Pitágoras fue introducido por el matemático griego Pitágoras de Samos. Fue un antiguo filósofo griego jónico. Formó un grupo de matemáticos que trabajaba religiosamente en los números y vivía como monjes. Finalmente, el matemático griego enunció el teorema, por lo que se le dio el nombre de «teorema de Pitágoras». Aunque fue introducido hace muchos siglos, su aplicación en la época actual es obligatoria para hacer frente a situaciones pragmáticas.
Aunque Pitágoras introdujo y popularizó el teorema, hay suficientes pruebas que demuestran su existencia en otras civilizaciones, 1000 años antes de que naciera Pitágoras. Las evidencias más antiguas que se conocen se remontan a los siglos XX al XVI a.C., en el período de la Antigua Babilonia.
Fórmula del Teorema de Pitágoras
La fórmula del teorema de Pitágoras afirma que en un triángulo rectángulo ABC, el cuadrado de la hipotenusa es igual a la suma del cuadrado de los otros dos catetos. Si AB y AC son los lados y BC es la hipotenusa del triángulo, entonces BC2 = AB2 + AC2. En este caso, AB es la base, AC es la altitud o la altura y BC es la hipotenusa.
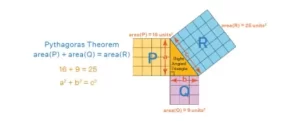
Otra forma de entender la fórmula del teorema de Pitágoras es utilizando la siguiente figura que muestra que el área del cuadrado formado por el lado más largo del triángulo rectángulo (la hipotenusa) es igual a la suma del área de los cuadrados formados por los otros dos lados del triángulo rectángulo.
En un triángulo rectángulo, la fórmula del Teorema de Pitágoras se expresa como
c2 = a2 + b2
Donde,
‘c’ = hipotenusa del triángulo rectángulo
‘a’ y ‘b’ son los otros dos catetos.
Demostración del Teorema de Pitágoras
El teorema de Pitágoras se puede demostrar de muchas maneras. Algunos de los métodos más comunes y utilizados son el método algebraico y el método de los triángulos semejantes. Veamos estos dos métodos individualmente para entender la demostración de este teorema.
Demostración de la fórmula del teorema de Pitágoras por el método algebraico
La prueba del teorema de Pitágoras se puede obtener mediante el método algebraico. Por ejemplo, utilicemos los valores a, b y c que se muestran en la siguiente figura y sigamos los pasos que se indican a continuación:
Demostración del teorema de Pitágoras por el método algebraico
Paso 1: Disponer cuatro triángulos rectángulos congruentes en el cuadrado dado PQRS, cuyo lado es a + b. Los cuatro triángulos rectángulos tienen ‘b’ como base, ‘a’ como altura y, ‘c’ como hipotenusa.
Paso 2: Los 4 triángulos forman el cuadrado interior WXYZ como se muestra, con ‘c’ como los cuatro lados.
Paso 3: El área del cuadrado WXYZ al disponer los cuatro triángulos es c2.
Paso 4: El área del cuadrado PQRS de lado (a + b) = Área de los 4 triángulos + Área del cuadrado WXYZ de lado ‘c’. Esto significa que (a + b)2 = [4 × 1/2 × (a × b)] + c2.Esto conduce a a2 + b2 + 2ab = 2ab + c2. Por tanto, a2 + b2 = c2. Por lo tanto, queda demostrado.
Demostración de la fórmula del teorema de Pitágoras mediante triángulos semejantes
Se dice que dos triángulos son semejantes si sus ángulos correspondientes son de igual medida y sus lados correspondientes están en la misma proporción. Además, si los ángulos son de la misma medida, entonces usando la ley del seno, podemos decir que los lados correspondientes también estarán en la misma proporción. Por lo tanto, los ángulos correspondientes en triángulos semejantes nos llevan a proporciones iguales de las longitudes de los lados.
Triángulos del Teorema de Pitágoras
Los triángulos rectángulos siguen la regla del teorema de Pitágoras y se llaman triángulos del teorema de Pitágoras. Los tres lados de un triángulo de este tipo se denominan colectivamente triángulos de Pitágoras. Todos los triángulos del teorema de Pitágoras siguen el teorema de Pitágoras que dice que el cuadrado de la hipotenusa es igual a la suma de los dos lados del triángulo rectángulo. Esto se puede expresar como c2 = a2 + b2; donde «c» es la hipotenusa y «a» y «b» son los dos catetos del triángulo.
Cuadrados del Teorema de Pitágoras
Según el teorema de Pitágoras, el área del cuadrado que se construye sobre la hipotenusa de un triángulo rectángulo es igual a la suma del área de los cuadrados construidos sobre los otros dos lados. Estos cuadrados se conocen como cuadrados de Pitágoras.
Aplicaciones del teorema de Pitágoras
Las aplicaciones del teorema de Pitágoras pueden verse en nuestro día a día. Estas son algunas de las aplicaciones del teorema de Pitágoras.
- Campos de la ingeniería y la construcción
La mayoría de los arquitectos utilizan la técnica del teorema de Pitágoras para encontrar las dimensiones desconocidas. Cuando se conoce la longitud o la anchura es muy fácil calcular el diámetro de un sector determinado. Se utiliza principalmente en dos dimensiones en los campos de la ingeniería. - Reconocimiento facial en cámaras de seguridad
La función de reconocimiento facial en las cámaras de seguridad utiliza el concepto del teorema de Pitágoras, es decir, se anota la distancia entre la cámara de seguridad y la ubicación de la persona y se proyecta bien a través de la lente utilizando el concepto. - Carpintería y diseño de interiores
El concepto de Pitágoras se aplica en el diseño de interiores y en la arquitectura de casas y edificios. - Navegación
Las personas que viajan por el mar utilizan esta técnica para encontrar la distancia y la ruta más cortas para dirigirse a sus lugares de interés.
Vídeos de Teorema de pitágoras fórmula
https://www.youtube.com/watch?v=w6nh99v3r4A
Contenido