Resta de vectores
La resta de vectores de dos vectores a y b se representa por a – b y no es más que sumar el negativo del vector b al vector a. Es decir, a – b = a + (-b). Así, la resta de vectores implica la suma de vectores y el negativo de un vector. El resultado de la resta de vectores es de nuevo un vector. Las reglas de la resta de vectores son las siguientes:
- Debe realizarse entre dos vectores solamente (no entre un vector y un escalar).
- Ambos vectores en la resta deben representar la misma cantidad física.
Sustracción de vectores por la ley del paralelogramo
Supongamos que a y b son dos vectores. ¿Cómo podemos interpretar gráficamente la resta de estos vectores? Es decir, ¿qué significado le damos a a – b? Para empezar, observamos que a – b será un vector que al sumarse a b debe devolver a. es decir
(a – b) + b = a
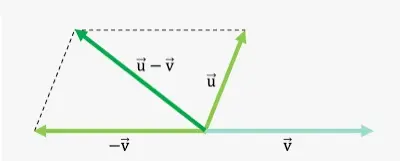
Utilizando la ley del paralelogramo de la suma de vectores, podemos determinar el vector de la siguiente manera. Interpretamos a – b como a + (- b), es decir, la suma vectorial de a y -b.
¿Cómo restar vectores?
Existen múltiples formas de restar vectores:
- Para restar dos vectores a y b gráficamente (es decir, para hallar a – b), basta con hacerlos coincidir primero y luego dibujar un vector desde la punta de b hasta la punta de a.
- Podemos añadir -b (el negativo del vector b que se obtiene multiplicando b por -1) a a para realizar la resta de vectores a – b. Es decir, a – b = a + (-b).
- Si los vectores están en forma de componentes podemos simplemente restar sus respectivos componentes en el orden de sustracción de vectores.
He aquí un ejemplo.
Ejemplo: Si a = <4, -2, 3> y b = <1, -2, 5> entonces encuentra a – b.
Solución:
a – b = <4, -2, 3> – <1, -2, 5>
= <4 – 1, -2 – (-2), 3 – 5>
= <3, 0, -2>
Por tanto, a – b = <3, 0, -2>.
Propiedades de la resta de vectores
He aquí algunas propiedades importantes de la resta de vectores.
- Cualquier vector restado de sí mismo da como resultado un vector cero, es decir, a – a = 0, para cualquier vector a.
- La resta de vectores NO es conmutativa. es decir, a – b no es necesariamente igual a b – a.
- La resta de vectores NO es asociativa. es decir, (a – b) – c no tiene por qué ser igual a a – (b – c).
(a – b) – (a + b) = |a|2 – |b|2.
(a – b) – (a – b) = |a – b|2 = |a|2 + |b|2 – 2 a – b.
Vídeos de Resta de vectores
Contenido