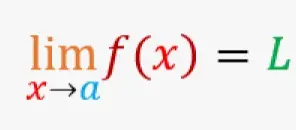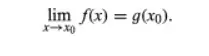Limites
Una forma de definir el límite de una función f(x) en un punto x0, escrito como
es la siguiente: si existe una función continua (no interrumpida) g(x) tal que g(x) = f(x) en algún intervalo alrededor de x0, excepto posiblemente en el propio x0, entonces
También se puede dar la siguiente definición más básica de límite, independiente del concepto de continuidad:
si, para cualquier grado de proximidad deseado ε, se puede encontrar un intervalo alrededor de x0 de modo que todos los valores de f(x) calculados aquí difieran de L en una cantidad menor que ε (es decir, si |x – x0| < δ, entonces |f (x) – L| < ε). Esta última definición puede utilizarse para determinar si un número dado es o no un límite. El cálculo de los límites, especialmente de los cocientes, suele implicar manipulaciones de la función para que pueda escribirse en una forma en la que el límite sea más obvio, como en el ejemplo anterior de (x2 – 1)/(x – 1).
Los límites son el método por el que se calcula la derivada, o tasa de cambio, de una función, y se utilizan en todo el análisis como una forma de convertir las aproximaciones en cantidades exactas, como cuando se define el área dentro de una región curva como el límite de las aproximaciones por rectángulos.
Propiedades de los limites
- limx→a c = c, donde c es una cantidad constante.
- El valor de limx→a x = a
- El valor de limx→a bx + c = ba + c
- El valor de limx→a xn = an, si n es un número entero positivo.
- Valor de limx→0+ 1/xr = +∞.
- limx→0- 1/xr = -∞, si r es impar, y
- limx→0- 1/xr = +∞, si r es par.
Vídeos de propiedades de los limites
Contenido