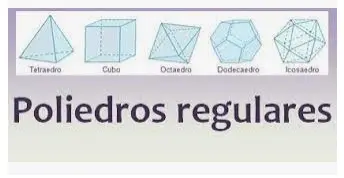
Poliedros regulares
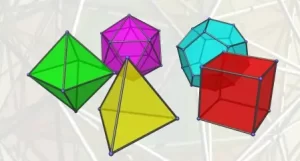
- El tetraedro regular, mostrado arriba en amarillo, está delimitado por 4 triángulos equiláteros. Es autodual: el casco convexo de los centros de sus caras es también un tetraedro regular.
- El cubo, mostrado arriba en rojo, está limitado por 6 cuadrados. Es dual al octaedro. El casco convexo de los centros de sus caras es el octaedro.
- El octaedro, mostrado arriba en verde, está limitado por 8 triángulos equiláteros. Es el dual del cubo.
- El dodecaedro, mostrado arriba en cian, está limitado por 12 pentágonos regulares y es dual del icosaedro.
- El icosaedro, mostrado arriba en magenta, está limitado por 20 triángulos equiláteros y es dual del dodecaedro.
Construcciones
Los 5 sólidos platónicos se pueden construir a partir del cubo.
El cubo
El cubo se construye fácilmente tomando todas las permutaciones de signo del punto
(1, 1, 1)
Estas coordenadas dan lugar a un cubo con longitud de arista 2.
El tetraedro
Una vez construido el cubo, podemos colorear cada uno de sus 8 vértices de rojo o verde, de forma que cada arista conecte un vértice rojo con un vértice verde. Por ejemplo, podemos asignar el rojo a los vértices que tienen un número par (incluido el 0) de signos negativos, y el verde a los vértices con un número impar de signos negativos. Así se forman dos grupos de vértices: 4 vértices rojos y 4 verdes. Si desechamos los vértices verdes, los 4 vértices rojos restantes forman un tetraedro. Esta operación se llama alternancia, y puede aplicarse a cualquier hipercubo de n dimensiones. Así, las coordenadas del tetraedro resultan ser (1,1,1) con todos los cambios de signo pares, es decir
(1, 1, 1)
(1, -1, -1)
(-1, 1, -1)
(-1, -1, 1)
El octaedro
Podríamos haber desechado los vértices rojos del cubo y quedarnos con los verdes en su lugar, y obtendríamos otro tetraedro que está en orientación dual con el primero. Los vértices de este tetraedro dual son los vértices del cubo con un número impar de signos negativos. La intersección de estos dos tetraedros nos da un octaedro. Como las aristas de los dos tetraedros duales se bisecan, los vértices del octaedro deben estar en sus puntos medios, que son todas las permutaciones de coordenadas y cambios de signo de:
(1, 0, 0)
El icosaedro
Ahora, los seis vértices del octaedro pueden agruparse en tres pares de opuestos; podemos colorearlos de rojo, verde y azul, respectivamente. Decide una ordenación cíclica de los colores, por ejemplo, rojo-verde-azul. Como cada cara del octaedro tendrá tres vértices de distinto color, podemos asignar una dirección a cada arista en función de nuestro ordenamiento cíclico: por ejemplo, podemos decir que el rojo va al verde, el verde al azul y el azul al rojo. Esta asignación de la dirección de las aristas se denomina «indexación coherente», y nos permite dividir cada arista en una proporción A:B según su dirección. Si dividimos cada una de las aristas del octaedro en la razón áurea, φ=(1+√5)/2, obtenemos los 12 vértices del icosaedro como todas las permutaciones pares de coordenadas de (0,±φ-1,±1), o si escalamos el icosaedro por un factor φ, todas las permutaciones pares de:
(0, ±1, ±φ)
El dodecaedro
Por último, tomando el dual del icosaedro, obtenemos el dodecaedro. Calculando los puntos medios de las caras del icosaedro se obtienen las coordenadas del dodecaedro, que, escaladas por un factor de 3φ2, son todas de cambios de signo de:
(1, 1, 1)
así como todas las permutaciones pares de coordenadas y todos los cambios de signo de:
(0, φ-1, φ)
Vídeos de Poliedros regulares
Contenido