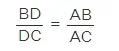Mediatriz de un triángulo
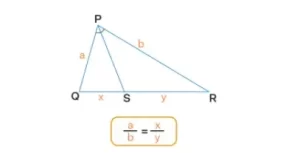
El teorema de la bisectriz del ángulo del triángulo afirma que en un triángulo, la bisectriz de cualquier ángulo dividirá el lado opuesto en la proporción de los lados que contienen el ángulo. Considera la figura siguiente:
Aquí, PS es la bisectriz de ∠P. Según el teorema de la bisectriz del ángulo, PQ/PR = QS/RS o a/b = x/y.
Una bisectriz de un ángulo es una línea o semirrecta que divide un ángulo de un triángulo en dos medidas iguales. Las principales propiedades de una bisectriz de un ángulo son que cualquier punto de la bisectriz de un ángulo es equidistante de los lados del ángulo y que la bisectriz de un ángulo divide el lado opuesto de un triángulo en la proporción de los lados adyacentes, lo que se conoce como la propiedad de la bisectriz de un ángulo.
Teorema inverso de la bisectriz del ángulo
El teorema de la bisectriz del ángulo dice que si los lados de un triángulo satisfacen la siguiente condición «Si una línea trazada desde un vértice de un triángulo divide el lado opuesto en dos partes tales que son proporcionales a los otros dos lados del triángulo», implica que el punto del lado opuesto de ese ángulo se encuentra en su bisectriz del ángulo. En este caso, sabemos que los lados son proporcionales, y a partir de esto, llegamos a la conclusión de que la línea/rayo/segmento es la bisectriz del ángulo respectivo. Esto se conoce como el teorema inverso de la bisectriz del ángulo en geometría.
Fórmula del teorema de la bisectriz del ángulo
El teorema de la bisectriz del ángulo del triángulo afirma que «En un triángulo, la bisectriz de cualquier ángulo dividirá el lado opuesto en la proporción de los lados que contienen el ángulo». A partir de esto, podemos escribir la fórmula del teorema del bisector del ángulo del triángulo como
Teorema del ángulo bisector Ejemplos
- Amy ha dibujado en la pizarra un triángulo ABC en el que AD es la línea trazada sobre el lado BC, donde, AB = 4 pulg, AC = 6 pulg, BD = 1,6 pulg y DC = 2,4 pulg. Ella quiere saber si AD es la bisectriz del ángulo de ∠A. ¿Puedes ayudarla?
Solución:
Para demostrar si AD es la bisectriz del ángulo o no, vamos a utilizar el teorema de la bisectriz del ángulo. Así, tenemos que demostrar que BD/DC = AB/AC.
Hallemos el cociente AB/AC.
AB/AC = 4/6 = 2/3
Busquemos el cociente BD/DC.
BD/DC = 1,6/2,4 = 2/3
Ambos cocientes son iguales.
Por tanto, en el triángulo dibujado por Amy, AD biseca a ∠A.
- En ΔXYZ, XE es la bisectriz de ∠X. Sea XY = 4 unidades, YE = 2 unidades y EZ = 3 unidades. ¿Puedes encontrar la longitud de XZ?
Solución:
Dado que, XE es la bisectriz de ∠X.
Según la fórmula del teorema del bisector del ángulo
YE/EZ = XY/XZ
2/3 = 4/XZ
XZ = 4/2 × 3
XZ = 6
Por lo tanto, la longitud de XZ = 6 unidades.
Vídeos de Mediatriz de un triángulo
Contenido