Matriz simétrica

por
Matriz simétrica
En álgebra lineal, una matriz simétrica se define como la matriz cuadrada que es igual a su matriz de transposición. La matriz de transposición de cualquier matriz A puede ser dada como AT. Por lo tanto, una matriz simétrica A satisface la condición, A = AT. Entre todos los tipos de matrices, las matrices simétricas son una de las más importantes que se utilizan ampliamente en el aprendizaje automático.

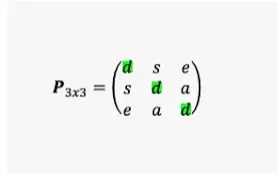
Matriz simétrica

Una matriz simétrica en álgebra lineal es una matriz cuadrada que permanece inalterada cuando se calcula su transposición. Es decir, una matriz cuya transposición es igual a la propia matriz, se llama matriz simétrica.

Una matriz cuadrada B que de tamaño n × n se considera simétrica si y sólo si BT = B. Consideremos la matriz dada B, es decir, una matriz cuadrada que es igual a la forma transpuesta de esa matriz, llamada matriz simétrica.

Ésta puede representarse como: Si B = [ b i j ] n × n es la matriz simétrica, entonces b i j = b j i para todo i y j o 1 ≤ i ≤ n, y 1 ≤ j ≤ n. Aquí n es cualquier número natural. b i j es un elemento en la posición (i, j) que es la iª fila y la jª columna de la matriz B y b j i es un elemento en la posición (j, i) que es la jª fila y la iª columna de la matriz B.

Propiedades de la matriz simétrica

Estas son algunas de las propiedades importantes de las matrices simétricas.

  • La suma y la diferencia de dos matrices simétricas dan la resultante como una matriz simétrica.
  • La propiedad anterior no siempre es cierta para el producto: Dadas las matrices simétricas A y B, entonces AB es simétrica si y sólo si A y B siguen la propiedad conmutativa de la multiplicación, es decir, si AB = BA.
  • Para un número entero n, si A es simétrica, ⇒ An es simétrica.
  • Si existe A-1, será simétrico si y sólo si A es simétrico.

Teoremas de las matrices simétricas

Hay dos teoremas importantes relacionados con la matriz simétrica. En esta sección, vamos a conocer estos teoremas junto con sus pruebas.

Teorema 1: Para cualquier matriz cuadrada B con elementos de números reales, B + BT es una matriz simétrica, y B – BT es una matriz sesgada-simétrica.

Demostración:

Sea A = B + BT.

Tomando una transposición, AT = ( B + BT )T = BT + ( BT )T = BT + B = B + BT = A

Esto implica que B + BT es una matriz simétrica.

A continuación, dejemos que C = B – BT

CT = ( B + ( – BT ))T = BT + ( – BT )T = BT – ( BT )T = BT- B = – ( B – BT ) = – C

Esto implica que B – BT es una matriz sesgada-simétrica.

Teorema 2: Cualquier matriz cuadrada puede expresarse como la suma de una matriz simétrica-oblicua y una matriz simétrica. Para hallar la suma de una matriz simétrica y otra asimétrica, utilizamos esta fórmula:

Sea B una matriz cuadrada. Entonces

B = (1/2) × (B + BT) + (1/2 ) × (B – BT). Aquí, BT es la transposición de la matriz cuadrada B.

  • Si B + BT es una matriz simétrica, entonces (1/2) × (B + BT) es también una matriz simétrica
  • Si B – BT es una matriz asimétrica, entonces (1/2 ) × (B – BT) es también una matriz asimétrica
  • Por lo tanto, cualquier matriz cuadrada puede expresarse como la suma de una matriz simétrica y una matriz simétrica.

Vídeos de Matriz simétrica

Contenido