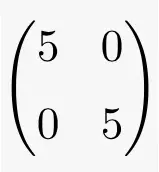
Matriz escalar
Una matriz escalar es un tipo de matriz cuadrada en la que sus elementos diagonales principales son todos iguales y los elementos no diagonales son todos . Es una constante multiplicativa de una matriz identidad.
Una matriz identidad es una matriz cuadrada en la que todas sus diagonales son -s, y el resto de sus elementos son 0.
- La propiedad asociativa establece que si una matriz se multiplica por dos escalares, podemos multiplicar primero los escalares y multiplicar esa constante por la matriz. O bien, podemos multiplicar la matriz por un escalar y luego volver a multiplicarla por el otro escalar.
- Distributiva dice que un escalar multiplicado con la suma de dos matrices puede distribuirse sobre la suma de matrices.
- Multiplicativa de la Identidad afirma que al multiplicar una matriz por el escalar 1 se obtiene la matriz original.
- Multiplicativa del Cero establece que multiplicar cualquier matriz por el escalar 0 da como resultado una matriz cero (una matriz cero es una matriz donde todos sus elementos son s).
Operaciones con matrices escalares
Una de las razones por las que las matrices escalares son tan utilizadas en el álgebra lineal es la facilidad con la que permiten realizar cálculos. Por eso son tan importantes en matemáticas. Veamos por qué es tan fácil hacer cálculos con este tipo de matrices cuadradas:
Suma y resta de matrices escalares
La suma (y la resta) de dos matrices escalares es muy sencilla: basta con sumar (o restar) los números de las diagonales principales.
Multiplicación de matrices escalares
De forma similar a la suma y la resta, para resolver una multiplicación o un producto matricial entre dos matrices escalares, sólo hay que multiplicar los elementos de las diagonales entre sí.
Potencia de matrices escalares
El cálculo de la potencia de una matriz escalar también es muy fácil: tenemos que elevar cada elemento de la diagonal al exponente.
Qué es una multiplicación escalar
Dado que una multiplicación escalar es una operación muy sencilla y que ya hemos hablado de ella anteriormente, esta sección puede parecer un poco redundante, pero la mantenemos para que no tengas que estar pinchando hacia adelante y hacia atrás entre esta lección y las anteriores si quieres ver los conceptos básicos. La multiplicación escalar se refiere a la operación en la que un número real multiplica un objeto algebraico como un vector o una matriz. Por supuesto, nos centramos en los casos de multiplicación de escalares y matrices juntos, ya que estamos trabajando en operaciones con matrices.
Recuerda que un escalar es un número real que multiplicado a un espacio vectorial «redimensiona» el vector (cambia su magnitud) sin afectar a su dirección. El nombre de «escalar» viene de esa operación en particular porque al multiplicar un número real por un vector se «reescala» el vector sin cambiar otras de sus características principales, como la dirección y las dimensiones. Pero como hemos dicho, nos interesa el caso en el que un escalar multiplica una matriz.
Así, la multiplicación escalar de una matriz produce un efecto similar al de la multiplicación de un escalar y un vector. La operación de la multiplicación de una matriz por un número real produce una matriz que mantiene sus principales propiedades como son: el orden, la dependencia lineal, la proporción entre sus elementos y la equivalencia entre los conjuntos de ecuaciones lineales que la pueden conformar.
Dado que una matriz es una matriz de números que puede pensarse como una matriz de vectores ordenados (ya sean vectores columna o vectores fila). Podemos utilizar esa relación y ver que una multiplicación matricial por números escalares da como resultado un array (la matriz resultante) de vectores ordenados que han tenido un cambio de magnitud (al igual que la multiplicación de un vector aislado por un escalar) pero siguen manteniendo la proporción entre sus diferentes coeficientes variables, o lo que es lo mismo, mantienen la misma dirección que tendrían si se graficaran en planos de coordenadas euclidianas.
Vídeos de Matriz escalar
Contenido