Longitud de una circunferencia
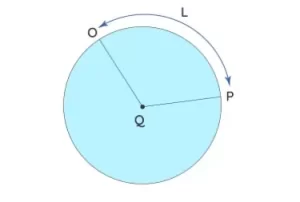
La longitud de arco se define como el espacio intermedio entre los dos puntos a lo largo de una sección de una curva. Un arco de círculo es cualquier parte de la circunferencia. El ángulo subtendido por un arco en cualquier punto es el ángulo formado entre los dos segmentos de línea que unen ese punto con los puntos extremos del arco. Por ejemplo, en la circunferencia que se muestra a continuación, OP es el arco de la circunferencia con centro Q. La longitud de este arco OP se da como L.
Fórmula de la longitud de arco
La longitud de un arco puede ser calculada usando diferentes fórmulas, basadas en la unidad del ángulo central del arco. Las medidas del ángulo central pueden estar dadas en grados o en radianes, y de acuerdo con ello, calculamos la longitud de arco de una circunferencia. Para un círculo, la fórmula de la longitud de arco es θ veces el radio de un círculo.
La fórmula de la longitud de arco en radianes se puede expresar como, longitud de arco = θ × r, cuando θ está en radianes. Longitud de Arco = θ × (π/180) × r, cuando θ está en grados, donde,
L = Longitud de un arco
θ = Ángulo central del arco
r = Radio del círculo
Fórmula de la longitud del arco en radianes
La longitud de arco de una circunferencia se puede calcular utilizando diferentes fórmulas, basadas en la unidad del ángulo central del arco. La fórmula de la longitud de arco en radianes puede expresarse como
Longitud de Arco = θ × r
donde,
L = Longitud del arco
θ = Ángulo central del arco en radianes
r = Radio del círculo
¿Cómo encontrar la longitud de arco de una curva?
La longitud de arco de una circunferencia puede ser calculada usando diferentes métodos y fórmulas basadas en los datos dados. Algunos casos importantes se dan a continuación,
- encontrar la longitud del arco con el radio y el ángulo central
- encontrar la longitud del arco sin el radio
- encontrar la longitud del arco sin el ángulo central
¿Cómo encontrar la longitud de arco con el radio y el ángulo central?
La longitud de arco de una circunferencia se puede calcular con el radio y el ángulo central utilizando la fórmula de la longitud de arco,
- Longitud de un arco = θ × r, donde θ está en radianes.
- Longitud de un arco = θ × (π/180) × r, donde θ está en grados.
¿Cómo encontrar la longitud del arco sin el radio?
La longitud de arco de una circunferencia se puede calcular sin el radio utilizando:
El ángulo central y el área del sector:
- Multiplicar el área del sector por 2 y además, dividir el resultado por el ángulo central en radianes.
- Hallar la raíz cuadrada del resultado de la división.
- Multiplique esta raíz obtenida por el ángulo central de nuevo para obtener la longitud de arco.
- Las unidades de esta longitud de arco calculada serán la raíz cuadrada de las unidades del área del sector.
Ejemplo
Calcular la longitud de arco de una curva con área de sector 25 unidades cuadradas y el ángulo central como 2 radianes.
Tenemos,
Área del sector = 25 unidades
Ángulo central = 2 radianes
Paso 1: Área del sector × 2 = 25 × 2 = 50
Paso 2: 50/ángulo central = 50/2 = 25
Paso 3: √25 = 5
Paso 4: 5 × ángulo central = 5 × 2 = 10 unidades
Por lo tanto, la longitud del arco = 10 unidades
Ángulo central y la longitud de la cuerda:
Dividir el ángulo central en radianes por 2 y además, realizar la función seno en él.
Divida la longitud de la cuerda dada por el doble del resultado del paso 1. Este cálculo da como resultado el radio.
Multiplique el radio por el ángulo central para obtener la longitud de arco.
Vídeos de Longitud de una circunferencia
Contenido