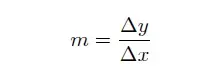Interpretacion geometrica de la derivada
Para entender la intuición geométrica de la derivada, necesitamos revisar un concepto del álgebra: la pendiente. En los cursos normales de cálculo se supone que se tiene un sólido conocimiento de este concepto.
Sin embargo, según mi experiencia, la mayoría de los estudiantes que llegan al nivel de cálculo no tienen el conocimiento necesario de él. Es tan importante para una verdadera comprensión de la derivada y para aplicarla a la resolución de problemas, que considero que merece la pena dedicar al menos dos minutos a repasarla.
Para empezar, consideremos una línea recta, como la que se muestra en el gráfico siguiente:
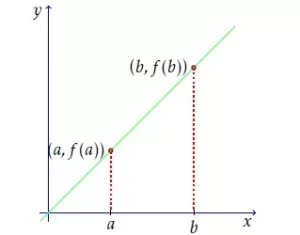
Esta recta es la gráfica de una función y=f(x). Vamos a dar una definición matemática de la pendiente. Tomamos dos puntos de la recta, correspondientes a los valores x=a, y x=b
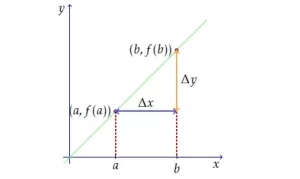
Ahora, vamos a denotar la distancia horizontal entre a y b por Δx. Esto se escribe «delta x». Y vamos a denotar la distancia vertical entre f(a) y f(b) por Δy («delta y»). Estas distancias se muestran a continuación:
En el cálculo nos gusta utilizar la letra Δ para denotar el «incremento», «cambio» o «variación» de algo. Así, por ejemplo, Δx es el cambio en x entre x=a y x=b. En este caso, Δx=b-a.
Del mismo modo, Δy es el cambio en y a lo largo de la línea, también entre x=a y x=b. En este caso, Δy = f(b) – f(a).
Ahora estamos preparados para definir la pendiente de la recta. Definimos la pendiente como el siguiente cociente:
Este número es independiente de los puntos a y b que elijamos. Es un cociente que es constante a lo largo de la línea. Y esta definición de pendiente tiene un sentido intuitivo. Veamos por qué.
Una recta que tenga una mayor pendiente (línea más empinada) corresponderá a un cociente mayor entre los deltas, porque en este caso Δy será mucho mayor que Δx. Si el cociente es pequeño, significa que Δy es mucho menor que Δx.
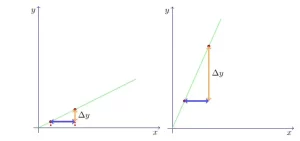
Por ejemplo, en la figura siguiente, mostramos dos líneas. En las dos, tomamos una Δx de la misma longitud. Puedes ver que a la primera línea le corresponde un Δy más pequeño. Por lo tanto, el cociente m será mucho menor para la primera línea. Esto corresponde a nuestra intuición de la inclinación: claramente la segunda línea es más inclinada que la primera, por lo que su pendiente es mayor.
La idea geométrica de la derivada no es más que una generalización del concepto de pendiente. Llegamos al concepto que llamamos derivada cuando intentamos calcular la pendiente de una curva que no es una línea recta.
La definición geométrica de derivada a la que llegaremos se parecerá mucho a la definición anterior de pendiente. La mayor diferencia será que implicará tomar un límite.
Vídeos de Interpretacion geometrica de la derivada
Contenido