Hiperbola

por
Hiperbola
En matemáticas, una hipérbola es una importante sección cónica formada por la intersección del doble cono por una superficie plana, pero no necesariamente en el centro. Una hipérbola es simétrica a lo largo del eje conjugado, y comparte muchas similitudes con la elipse. Conceptos como focos, directriz, latus rectum, excentricidad, se aplican a una hipérbola. Algunos ejemplos comunes de hipérbola son la trayectoria que sigue la punta de la sombra de un reloj de sol, la trayectoria de dispersión de las partículas subatómicas, etc.

Hiperbola

Una hipérbola, un tipo de curva suave situada en un plano, tiene dos piezas, llamadas componentes conectadas o ramas, que son imágenes especulares entre sí y se asemejan a dos arcos infinitos. Una hipérbola es un conjunto de puntos cuya diferencia de distancias a dos focos es un valor constante. Esta diferencia se toma de la distancia al foco más lejano y luego de la distancia al foco más cercano. Para un punto P(x, y) de la hipérbola y para dos focos F, F’, el lugar de la hipérbola es PF – PF’ = 2a.

Definición de la hipérbola

Una hipérbola, en geometría analítica, es una sección cónica que se forma cuando un plano interseca a un cono circular recto doble en un ángulo tal que ambas mitades del cono se intersectan. Esta intersección del plano y el cono produce dos curvas separadas no limitadas que son imágenes especulares la una de la otra llamadas hipérbola.

Partes de una hipérbola

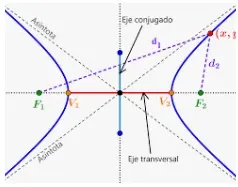
  • Focos de la hipérbola: La hipérbola tiene dos focos y sus coordenadas son F(c, o), y F'(-c, 0).
  • Centro de la hipérbola: El punto medio de la recta que une los dos focos se llama centro de la hipérbola.
  • Eje mayor: La longitud del eje mayor de la hipérbola es de 2a unidades.
  • Eje menor: La longitud del eje menor de la hipérbola es de 2b unidades.
  • Vértices: Los puntos en los que la hipérbola se cruza con el eje se llaman vértices. Los vértices de la hipérbola son (a, 0), (-a, 0).
  • Recto de la hipérbola: El recto de la hipérbola es una línea trazada perpendicularmente al eje transversal de la hipérbola y que pasa por los focos de la misma. La longitud del latus rectum de la hipérbola es 2b2/a.
  • Eje transversal: La línea que pasa por los dos focos y el centro de la hipérbola se llama eje transversal de la hipérbola.
  • Eje conjugado: La recta que pasa por el centro de la hipérbola y es perpendicular al eje transversal se llama eje conjugado de la hipérbola.
  • Excentricidad de la hipérbola: (e > 1) La excentricidad es el cociente entre la distancia del foco al centro de la hipérbola, y la distancia del vértice al centro de la hipérbola. La distancia del foco es ‘c’ unidades, y la distancia del vértice es ‘a’ unidades, y por lo tanto la excentricidad es e = c/a.

Vídeos de Hiperbola

Contenido