Función racional
La función racional es el cociente de dos funciones polinómicas cuyo polinomio denominador no es igual a cero. Se suele representar como R(x) = P(x)/Q(x), donde P(x) y Q(x) son funciones polinómicas. En cursos anteriores, aprendimos el concepto de número racional. Es el cociente o razón de dos números enteros, donde el denominador no es igual a cero. De ahí que el nombre de racional se derive de la palabra cociente.
Definición de función racional
Un número que se puede expresar en la forma de p/q
donde p y q son números enteros y q ≠ 0, es un número racional.
Al igual que los números racionales, la definición de función racional como:
Definición: Una función racional R(x) es la función de la forma P(x)/Q(x) donde P(x) y Q(x) son funciones polinómicas y Q(x) es un polinomio distinto de cero.
De la condición dada para Q(x), podemos concluir que los ceros de la función polinómica en el denominador no caen en el dominio de la función. Cuando Q(x) = 1, es decir, una función polinómica constante, la función racional se convierte en una función polinómica.
Gráficas de funciones racionales
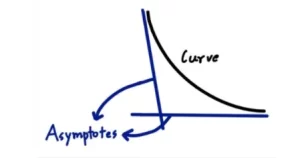
Un concepto muy importante para graficar funciones racionales es conocer sus asíntotas. Una asíntota es una línea o curva que se aproxima a la curva para siempre pero que nunca la toca.
Asíntotas de las funciones racionales
Las funciones racionales pueden tener 3 tipos de asíntotas:
- Asíntotas horizontales
- Asíntotas verticales
- Asíntota oblicua
- Asíntotas horizontales
Esto significa literalmente que la asíntota es horizontal, es decir, paralela al eje de la variable independiente. R(x) sólo puede tener una asíntota horizontal si
Grado de P(x) ≤ Grado de Q(x)
Una función racional es un cociente de polinomios donde el polinomio del denominador no debe ser igual a cero. ¿No se parece a la definición de número racional (que es de la forma p/q, donde q ≠ 0)? ¿Sabías que las funciones racionales encuentran aplicación en diferentes campos de nuestra vida cotidiana? No sólo describen la relación entre la velocidad, la distancia y el tiempo, sino que también son muy utilizadas en la industria médica y de la ingeniería.
¿Qué es una función racional?
Una función racional es una función que es el cociente de polinomios. Cualquier función de una variable, x, se llama función racional si, puede representarse como f(x) = p(x)/q(x), donde p(x) y q(x) son polinomios tales que q(x) ≠ 0. Por ejemplo, f(x) = (x2 + x – 2) / (2×2 – 2x – 3) es una función racional y aquí, 2×2 – 2x – 3 ≠ 0.
Sabemos que toda constante es un polinomio y, por tanto, los numeradores de una función racional pueden ser también constantes. Por ejemplo, f(x) = 1/(3x+1) puede ser una función racional. Pero ten en cuenta que los denominadores de las funciones racionales no pueden ser constantes. Por ejemplo, f(x) = (2x + 3) / 4 NO es una función racional, sino que es una función lineal.
Vídeos de Función racional
Contenido