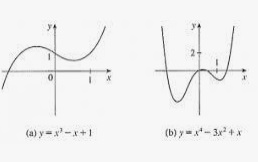
Función polinómica
Polinomio se compone de dos palabras, poly, y nomial. «Poly» significa muchos, y «nomial» significa el término, y por lo tanto cuando se combinan, podemos decir que los polinomios son «expresiones algebraicas con muchos términos». Vamos a empezar con la definición de las funciones polinómicas y sus tipos.
Definición de función polinómica
Las funciones polinómicas son expresiones que pueden contener variables de distintos grados, coeficientes, exponentes positivos y constantes. Estos son algunos ejemplos de funciones polinómicas.
f(x) = 3×2 – 5
g(x) = -7×3 + (1/2) x – 7
h(x) = 3×4 + 7×3 – 12×2
Función polinómica en forma estándar
Una función polinómica en forma estándar es: f(x) = a n xn + a n – 1 xn-1 + … + a 2 x2+ a 1 x + a 0 . Esta expresión algebraica se llama función polinómica en la variable x.
Aquí a n , a n – 1 , … a 0 son constantes de números reales a n no puede ser igual a cero y se llama coeficiente principal n es un número entero no negativo
Cada exponente de la variable en la función polinómica debe ser un número entero
La función polinómica en forma estándar es f de x igual a una expresión algebraica en x.
Grado de una función polinómica
El grado de la función polinómica es la mayor potencia de la variable a la que está elevada. Consideremos esta función polinómica f(x) = -7×3 + 6×2 + 11x – 19, el mayor exponente encontrado es 3 de -7×3. Esto significa que el grado de este polinomio en particular es 3.
Tipos de funciones polinómicas
El nombre de un polinomio viene determinado por el número de términos que contiene. Los tres polinomios más comunes que solemos encontrar son los monomios, los binomios y los trinomios.
- Los monomios son polinomios que contienen un solo término. Ejemplos: 15×2, 3b y 12y4
- Los binomios son polinomios que contienen sólo dos términos. Ejemplos: x + y, 4x – 7, y 9x + 2
- Los trinomios son polinomios que contienen sólo tres términos. Ejemplos: x3 – 3 + 5x, z4 + 45 + 3z, y x2 – 12x + 15
Además, los polinomios también se clasifican en función de sus grados. Los cuatro tipos más comunes de polinomios que se utilizan en pre-cálculo y álgebra son la función polinómica cero, la función polinómica lineal, la función polinómica cuadrática y la función polinómica cúbica.
Función polinómica cero
Una función polinómica cero es de la forma f(x) = 0, es decir, sólo contiene 0 y ningún otro término o variable. Como f(x) = una constante aquí, es una función constante.
Función polinómica lineal
Una función polinómica lineal tiene un grado 1. Es de la forma f(x) = ax + b. Algunos ejemplos de una función polinómica lineal son f(x) = x + 3, f(x) = 25x + 4, y f(y) = 8y – 3.
Función polinómica cuadrática
Una función polinómica cuadrática tiene un grado 2. Es de la forma f(x) = ax2 + bx + c. Algunos ejemplos de una función polinómica cuadrática son f(m) = 5m2 – 12m + 4, f(x) = 14×2 – 6, y f(x) = x2 + 4x.
Función polinómica cúbica
Una función polinómica cúbica tiene un grado 3. Es de la forma f(x) = ax3 + bx2 + cx + d. Algunos ejemplos de una función polinómica cúbica son f(y) = 4y3, f(y) = 15y3 – y2 + 10, y f(a) = 3a + a3.
Vídeos de Función polinómica
Contenido