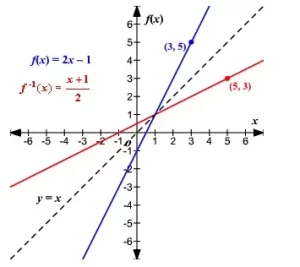
Función inversa
La función inversa se representa por f-1 con respecto a la función original f y el dominio de la función original se convierte en el rango de la función inversa y el rango de la función dada se convierte en el dominio de la función inversa. La gráfica de la función inversa se obtiene intercambiando (x, y) por (y, x) con referencia a la recta y = x.
Conozcamos más sobre la función inversa, los pasos para encontrar la función inversa y la gráfica de la función inversa.
¿Qué es la función inversa?
La inversa de una función f se denomina f-1 y sólo existe cuando f es una función unitaria y onto. Nótese que f-1 NO es el recíproco de f. La composición de la función f y la función recíproca f-1 da el valor del dominio de x.
(f o f-1) (x) = (f-1 o f) (x) = x
Para que una función ‘f’ se considere una función inversa, cada elemento en el rango y ∈ Y ha sido mapeado desde algún elemento x ∈ X en el conjunto de dominio, y tal relación se llama relación unívoca o relación de interdicción. También la inversa f-1 de la función dada tiene un dominio y ∈ Y se relaciona con un elemento distinto x ∈ X en el conjunto de codominio, y este tipo de relación con referencia a la función dada ‘f’ es una función onto o una función de suryección. Por lo tanto, la función inversa al ser una función injuntiva y una función de suryección, se llama función biyectiva.
Consideremos una función f cuyo dominio es el conjunto X y el codominio es el conjunto Y. La función f es invertible si existe otra función g cuyo dominio es Y y su codominio es X. Estas dos funciones pueden representarse como f(x) = Y, y g(y) = X. Para esta situación, si la función f(x) es inversa, entonces su función inversa g(x) es única.
Si la composición de dos funciones f(x), y g(x), da como resultado una función identidad f(g(x))= x, entonces se dice que las dos funciones son inversas entre sí. Si la aplicación de una función a x como entrada da n salida de y, entonces la aplicación de otra función g a y debe devolver el valor de x. Por tanto, la inversa de una función invierte la función. El dominio de la función dada se convierte en el rango de la función inversa, y el rango de la función dada se convierte en el dominio de la función inversa.
Para hallar la inversa de una función algebraicamente, intercambia la x y la y y resuelve para y .
Ejemplo de función inversa
Sea h(x)=x3+4
Sustituye h(x) por y e intercambia x e y :
y=x3+4x=y3+4
Resolver para y : x-4=y3
Vídeos de Función inversa
Contenido