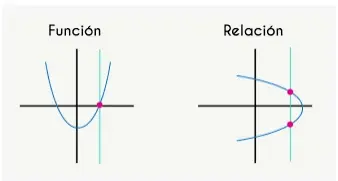
Función
¿Qué es una función? Una función se define como una relación entre un conjunto de entradas que tienen una salida cada una. En palabras sencillas, una función es una relación entre entradas en la que cada entrada está relacionada con una salida exactamente. Toda función tiene un dominio y un codominio o rango. Una función se suele denotar por f(x), donde x es la entrada. La representación general de una función es y = f(x).
¿Qué es una función en matemáticas?
Una función en matemáticas es una relación especial entre las entradas (es decir, el dominio) y sus salidas (conocido como el codominio) donde cada entrada tiene exactamente una salida y la salida puede ser rastreada hasta su entrada.
Tipos de funciones en matemáticas
Un ejemplo de función simple es f(x) = x2. En esta función, la función f(x) toma el valor de «x» y lo eleva al cuadrado. Por ejemplo, si x = 3, entonces f(3) = 9. Otros ejemplos de funciones son: f(x) = sen x, f(x) = x2 + 3, f(x) = 1/x, f(x) = 2x + 3, etc.
Hay varios tipos de funciones en matemáticas. Algunos tipos importantes son:
- Función inyectiva o función uno a uno: Cuando existe un mapeo para un rango para cada dominio entre dos conjuntos.
- Funciones suryectivas o función onto: Cuando hay mapeo de más de un elemento del dominio al rango.
- Función polinómica: La función que está formada por polinomios.
- Funciones inversas: La función que puede invertir otra función.
- Estos son algunos ejemplos de funciones. Hay que tener en cuenta que existen otras funciones, como la función «into», las funciones algebraicas, etc.
¿Qué es una función en álgebra?
Una función es una ecuación para la cual cualquier x que se pueda poner en la ecuación producirá exactamente una salida como y fuera de la ecuación. Se representa como;
y = f(x)
Donde x es una variable independiente e y es una variable dependiente.
Por ejemplo
y = 2x + 1
y = 3x – 2
y = 4y
y = 5/x
¿Qué es una función en una gráfica?
Una función f(x) se puede representar en una gráfica conociendo los valores de x. Como sabemos, y = f(x), por lo que si empezamos a poner los valores de x podemos obtener el valor correspondiente de y. Por lo tanto, podemos trazar una gráfica utilizando los valores de x e y en un plano de coordenadas. Veamos un ejemplo:
Supongamos que y = x + 3
Entonces
cuando x = 0, y = 3
cuando x = -2, y = -2 + 3 = 1
cuando x = -1, y = -1 + 3 = 2
cuando x = 1, y = 1 + 3 = 4
cuando x = 2, y = 2 + 3 = 5
Así, con la ayuda de estos valores, podemos trazar la gráfica de la función x + 3.
Vídeos de Función
Contenido