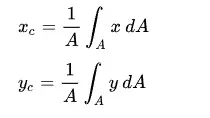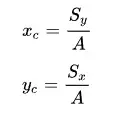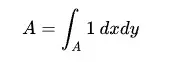Formulario de centroides
El punto correspondiente al centro geométrico de un objeto se conoce como centroide. Dependiendo de la forma del objeto, pueden ser necesarias una, dos o tres coordenadas para definir su posición exacta en el espacio. Si una forma posee un eje de simetría, su centroide estará siempre situado en ese eje. Si tiene dos o varios ejes de simetría, su centroide coincidirá con la intersección de dichos ejes.
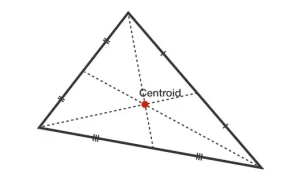
El centroide de un triángulo es la intersección de las tres medianas, o la «media» de los tres vértices. Tiene varias propiedades y relaciones importantes con otras partes del triángulo, como su circuncentro, ortocentro, incentro, área, etc.
El centroide de cualquier forma se puede encontrar mediante integración, siempre que su borde se describa como un conjunto de funciones matemáticas integrables. En concreto, las coordenadas del centroide xc e yc de un área A, vienen dadas por las dos fórmulas siguientes:
El término integral de las dos últimas ecuaciones también se conoce como «momento estático» o «primer momento» del área, que suele simbolizarse con la letra S. Por tanto, las últimas ecuaciones pueden reescribirse de esta forma:
El área A también se puede encontrar a través de la integración, si es necesario:
El primer momento del área S se define siempre alrededor de un eje y, convencionalmente, el nombre de ese eje se convierte en el índice. Por ejemplo, Sx es el primer momento del área en torno al eje x. Así, no es extraño que el primer momento, Sx, se utilice para la coordenada del centroide yc , ya que la coordenada y es en realidad la medida de la distancia al eje x.
‘Momento estático’ y ‘primer momento del área’ son términos equivalentes. Se puede utilizar cualquiera de los dos, aunque en algunas disciplinas de la ingeniería prevalece el «momento estático».
Pasos para encontrar el centroide mediante fórmulas de integración
Los pasos para el cálculo de las coordenadas del centroide, xc e yc , mediante integración, se resumen a lo siguiente
- Seleccionar un sistema de coordenadas, (x,y), con el que medir la ubicación del centroide.
- Seleccione un sistema de coordenadas apropiado y conveniente para la integración. Puede ser el mismo (x,y) o uno diferente. En lo sucesivo se llamará sistema de coordenadas de trabajo.
- Describir los bordes de la forma y las variables x, y según el sistema de coordenadas de trabajo.
- Integrar, sustituyendo, cuando sea necesario, las variables x e y con sus definiciones en el sistema de coordenadas de trabajo.
Vídeos de Formulario de centroides
Contenido