Perimetro del rectangulo
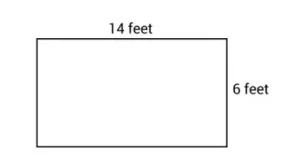
La fórmula del perímetro de un rectángulo dice que P = (L + W) × 2, donde P representa el perímetro, L la longitud y W la anchura. Si te dan las dimensiones de un rectángulo, puedes introducir los valores de L y W en la fórmula para resolver el perímetro. Por ejemplo, si el rectángulo de abajo representa un jardín que necesita un borde de ladrillo, podemos utilizar la fórmula del perímetro para determinar cuántos pies de borde de ladrillo necesitamos en total.
Fórmula del perímetro del rectángulo
La fórmula establece que P = (L + W) × 2, así que introduzcamos 14 pies para L y 6 pies para W. Ahora tenemos P = (14 + 6) × 2, que se simplifica a 40, o 40 pies.
El uso de la fórmula del perímetro nos ahorra un poco de tiempo al evitar la estrategia alternativa que sería sumar la longitud de cada lado por separado. 14 + 6 + 14 + 6 daría la respuesta correcta, pero esta estrategia suele llevar más tiempo, por lo que se recomienda utilizar la fórmula.
Sin embargo, no todos los problemas de perímetro le proporcionarán la longitud y la anchura de forma tan directa. De hecho, algunos problemas de perímetro te proporcionarán una dimensión y el área del rectángulo. Para resolver este tipo de problemas de perímetro tenemos que repasar nuestra comprensión del área. Recuerda que para calcular el área de un rectángulo, simplemente multiplicamos la longitud por la anchura. Un rectángulo que mide 3,5 cm por 4 cm tendría un área de 14 cm2 porque 3,5 × 4 = 14. Utilicemos este conocimiento del área y apliquémoslo a un problema de perímetro.
Por ejemplo, supongamos que necesitamos enmarcar una ventana rectangular grande que tiene un área de 35 pies cuadrados y una longitud de 7 pies. Utilicemos lo que sabemos sobre el cálculo del área para encontrar el perímetro.
Sabemos que la superficie se halla multiplicando la longitud por la anchura. Esto significa que 7 multiplicado por algo es igual a 35, 7 × ? = 35. Podemos resolver la longitud lateral que falta dividiendo 35 entre 7, que es igual a 5. Ahora podemos aplicar la fórmula del perímetro porque sabemos que la longitud es de 7 pies y la anchura es de 5 pies.
P = (L + W) × 2 se convierte en P = (7 + 5) × 2, lo que se simplifica en 24, es decir, 24 pies.
Ahora que hemos revisado la fórmula del perímetro y sus diversas aplicaciones, considera la siguiente pregunta. ¿Un rectángulo con un área de 20 pies cuadrados tiene más de una opción posible para su perímetro? Si has respondido que sí, estás en lo cierto. Los rectángulos con un área restringida como 20 pies cuadrados pueden tener una variedad de perímetros. Por ejemplo, un rectángulo de 20 pies cuadrados podría tener las dimensiones de 1 pie × 20 pies, 2 pies × 10 pies o 4 pies × 5 pies. Todas estas opciones producirán un perímetro diferente aunque todas tengan la misma área. Probemos este concepto calculando el perímetro de los tres posibles rectángulos que acabamos de mencionar: 1 pie × 20 pies, 2 pies × 10 pies y 4 pies × 5 pies.
1 pie × 20 pies: P = (L + W) × 2 = (1 + 20) × 2 = 42 pies
2 pies × 10 pies = L + W × 2 = (2 + 10) × 2 = 24 pies
4 pies × 5 pies = L + W × 2 = 4 + 5 × 2 = 18 pies
*También es importante tener en cuenta que la fórmula P = (L + W) × 2 sólo se aplica a los rectángulos. Esta fórmula sólo funciona para cuadriláteros que tienen dos conjuntos de lados congruentes.
Vídeos de Formula del perimetro del rectangulo
https://www.youtube.com/watch?v=l3ZydJ4RGjM
Contenido