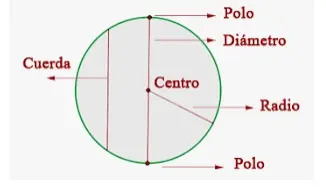
Elementos de la esfera
Una esfera es un homólogo tridimensional de un círculo, con todos sus puntos situados en el espacio a una distancia constante del punto fijo o del centro, llamado radio de la esfera. El radio de la esfera se denota como r.
El diámetro de una esfera: La línea que pasa por el centro de un extremo a otro se llama diámetro de la esfera. El diámetro de la esfera se denomina D.
Diámetro = 2 veces el radio de la esfera
D = 2 × r
Circunferencia de una esfera: La circunferencia de una esfera es la distancia recorrida alrededor de la esfera. La unidad de la circunferencia es la misma que la del radio.
Circunferencia = 2×π×r
La superficie de una esfera: La superficie de una esfera es el número de unidades cuadradas que cubren exactamente la superficie de una esfera. La unidad de la superficie de la esfera es la unidad cuadrada m²
La superficie de una esfera es
Superficie de la esfera = 4 veces el área de un círculo
Superficie de la esfera =4×π×r2
El volumen de una esfera: El volumen de la esfera es el número de unidades cúbicas que llenan una esfera. La unidad de volumen de la esfera es una unidad cúbica m³
El volumen que encierra una esfera es
Volumen de la esfera = 4/3π r³
Ejemplo de Elementos de la esfera
El radio de la esfera es de 5 cm. Halla el diámetro, la circunferencia, la superficie y el volumen de una esfera.
Solución: Dado que r = 5 cm
Diámetro de una esfera = 2 × r
= 2 × 5
=10 cm
Circunferencia de una esfera = 2×π×r
= 2×π×5
= 31,41 cm
Superficie de la esfera =4×π×r2
= 4×π×52
= 4××3.14×25
= 314,16 cm²
¿Cómo encontrar el volumen de una esfera?
- Paso 1: Revisa bien los datos que se dan en la pregunta.
- Paso 2: Comprueba qué valor se da: radio, diámetro, superficie o circunferencia.
- Paso 3: Encuentre el radio de la esfera. Si se da el diámetro, divídelo por 2 para encontrar el radio. Si se da el área de la superficie, encuentre el valor del radio a partir de la fórmula del área de la superficie de una esfera 4r. Si se da la circunferencia, halle el radio a partir de la fórmula 2r.
- Paso 4: Repasa las unidades con cuidado. Convierta todas las unidades equivalentes entre sí en una sola forma.
- Paso 5: Obtenga el cubo del radio, es decir, r³.
- Paso 6: Multiplica el valor de r³ por .
- Paso 7: Multiplique el valor encontrado en el Paso 6 por 4/3.
- Paso 8: El valor final será el volumen necesario de una esfera.
Vídeos de Elementos de la esfera
Contenido