Ecuaciones de la recta
La ecuación de una recta se suele escribir como y=mx+b, donde m es la pendiente y b es la intersección.
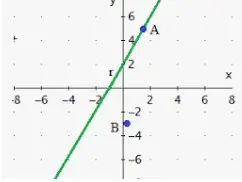
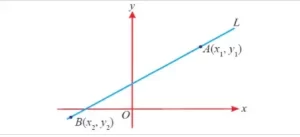
Si conoces dos puntos por los que pasa una recta, esta página te mostrará cómo encontrar la ecuación de la recta.
Las ecuaciones de las líneas tienen las siguientes formas:
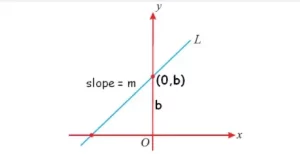
Forma de intercepción de la pendiente
y = m x + b
La forma de intercepción de la pendiente es útil si se conocen la pendiente m y la intercepción y (0, b).
La ecuación de una recta con pendiente -2 e intercepción y (0 , 3) se escribe como sigue
y = – 2 x + 3
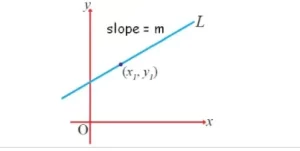
Forma de la pendiente del punto
y – y1 = m (x – x1)
La forma de pendiente puntual es útil si se conoce la pendiente m y un punto (x1 , y1) por el que pasa la recta.
La ecuación de una recta que pasa por el punto (5 , 7) y tiene pendiente – 3 puede escribirse como sigue
y – 7 = – 3 (x – 7)
Ecuación de una recta vertical
x = k , donde k es una constante.
La ecuación de una recta vertical que pasa por el punto (-2 , -5) puede escribirse como sigue
x = – 2
Ecuación de una recta horizontal
y = k , donde k es una constante.
La ecuación de una recta horizontal que pasa por el punto (-2 , -5) puede escribirse como sigue
y = – 5
Ecuación general de una recta
a x + b y = c , donde a, b y c son constantes.
Ecuación general de una recta:
2 x – 5 y = 8
Vídeos de Ecuaciones de la recta
Contenido