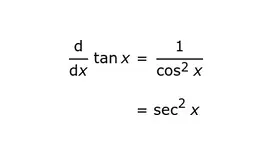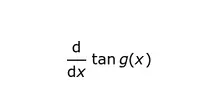Derivada tangente
La diferenciación de funciones trigonométricas es el proceso matemático de hallar la derivada de una función trigonométrica, o su tasa de cambio con respecto a una variable. Las funciones trigonométricas más comunes son sin(x), cos(x) y tan(x). Por ejemplo, la derivada de f(x) = sin(x) se representa como f ′(a) = cos(a). f ′(a) es la tasa de cambio de sin(x) en un punto concreto.
Ahora sabemos que la derivada de sen x es cos x y la derivada de cos x es -sin x. Sustituyendo estas derivadas en los paréntesis y simplificando, obtenemos:
Ahora hay dos identidades trigonométricas que podemos utilizar para simplificar este problema:
sin2x + cos2x = 1
sec x = 1/cos x
Y ya está, ¡hemos terminado! La derivada de tan x es sec2x.
Sin embargo, puede haber más cosas para encontrar derivadas de la tangente. En el caso general, tan x es la tangente de una función de x, como tan g(x). Observa que en el caso simple, g(x) = x.
En general, lo que buscamos es:
Todas las derivadas de las funciones trigonométricas circulares se pueden encontrar utilizando las de sen(x) y cos(x). A continuación, se aplica la regla del cociente para diferenciar la expresión resultante. Encontrar las derivadas de las funciones trigonométricas inversas implica utilizar la diferenciación implícita y las derivadas de las funciones trigonométricas regulares.
La derivada de tan x con respecto a x se denota por d/dx (tan x) (o) (tan x)’ y su valor es igual a sec2x. Tan x es diferenciable en su dominio. Para demostrar que la diferenciación de tan x es sec2x, utilizamos las identidades trigonométricas existentes y las reglas de diferenciación existentes. Podemos demostrarlo de las siguientes maneras:
- Prueba por primer principio
- Prueba por la regla de la cadena
- Prueba por la regla del cociente
Fórmula de la derivada de Tan x
La fórmula para la diferenciación de tan x es
d/dx (tan x) = sec2x (o)
(tan x)’ = sec2x
La derivada de tan x es sec al cuadrado de x. Se denota como tan x elevado a d o d sobre d x de tan x.
Ahora demostraremos esto en diferentes métodos en las próximas secciones.
Derivada de Tan x Prueba por primer principio
Para encontrar la derivada de tan x, suponemos que f(x) = tan x. Entonces, por primer principio, su derivada viene dada por el siguiente límite
Por tanto, queda demostrado.
Derivada de Tan x Demostración por la regla de la cadena
Demostraremos la fórmula de la diferenciación de tan x por la regla de la cadena. Para ello observemos que podemos escribir y = tan x como y = 1 / (cot x) = (cot x)-1. Ahora, por la regla de la potencia y la regla de la cadena
y’ = (-1) (cot x)-2 – d/dx (cot x)
Tenemos que d/dx (cot x) = -csc2x. Además, por una propiedad de los exponentes, a-m = 1/am.
y’ = -1/cot2x – (-csc2x)
y’ = tan2x – csc2x
Ahora, tan x = (sen x)/(cos x) y csc x = 1/(sen x). Así que
y’ = (sen2x)/(cos2x) – (1/sin2x)
= 1/cos2x
Tenemos que 1/cos x = sec x. Así que
y’ = sec2x
Por lo tanto, se ha demostrado.
Derivada de Tan x Prueba por la regla del cociente
Podemos aplicar la regla del cociente para obtener la fórmula de la derivada de tan x. Para ello, tenemos que escribir tan x como una fracción. Sabemos que tan x = (sen x)/(cos x). Así que suponemos que y = (sen x)/(cos x). Entonces, por la regla del cociente
y’ = [ cos x – d/dx (sin x) – sin x – d/dx (cos x)] / (cos2x)
= [cos x – cos x – sin x (-sin x)] / (cos2x)
= [cos2x + sin2x] / (cos2x)
Por una de las identidades pitagóricas, cos2x + sin2x = 1. Así que
y’ = 1 / (cos2x) = sec2x
Por lo tanto, se ha demostrado. Esta prueba es la más fácil de todas las pruebas de las derivadas de tan x.
Vídeos de Derivada tangente
Contenido