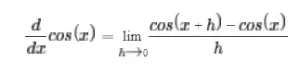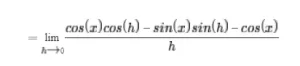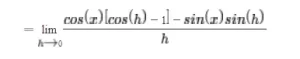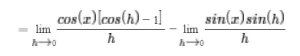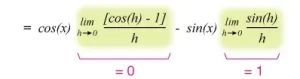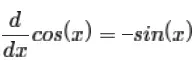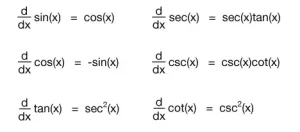Derivada del coseno
Las fórmulas de las derivadas para incluir las derivadas de estas y otras funciones trigonométricas. Comenzamos con las derivadas de las funciones seno y coseno y luego las utilizamos para obtener las fórmulas de las derivadas de las cuatro funciones trigonométricas restantes. Ser capaz de calcular las derivadas de las funciones seno y coseno nos permitirá encontrar la velocidad y la aceleración del movimiento armónico simple.
La derivada de f(x) = cos(x)
Encontramos la derivada de f(x) = cos(x) de una manera similar, y voy a trabajar a través de todo el asunto de nuevo aquí. Empieza con la expresión del cociente de la diferencia,
entonces sustituye cos(x + h) por cos(x)cos(h) – sin(x)sin(h):
Ahora mueve el factor común cos(x) y reescribe el numerador:
Divide la expresión en dos límites:
y eliminar las expresiones no dependientes de h para encontrar nuestros conocidos límites trigonométricos:
Esta vez tenemos:
Derivadas de las funciones trigonométricas
Aquí tienes las derivadas de las seis funciones trigonométricas. Debes memorizar las derivadas de sen(x), cos(x) y tan(x):
Vídeos de Derivada del coseno
Contenido