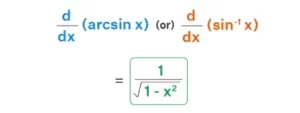Derivada del arcoseno

Para encontrar la derivada de arcsin, tenemos que considerar algunos hechos sobre arcsin. arcsin (que también se puede escribir como sin-1) es la función inversa de la función seno. es decir, Si y = sin-1x entonces sin y = x. Por la definición de funciones inversas, si f y f-1 son funciones inversas entre sí entonces f(f-1(x)) = f-1(f(x)) = x. De esto, sin(arcsin x) = arcsin(sin x) = x en los dominios correspondientes. Utilizamos estos hechos para encontrar la derivada de arcsin x.

Derivada del arcoseno

La derivada de arcsin x se denota por d/dx(arcsin x) (o) d/dx(sin-1x) (o) (arcsin x)’ (o) (sin-1x)’. Su valor es 1/√1 – x². Lo demostraremos por dos métodos en los próximos apartados. Los dos métodos son

Utilizando la regla de la cadena
Utilizando los primeros principios
Fórmula de la derivada de arcsin x
La derivada de la función arcsin es,

d/dx(arcsin x) = 1/√1 – x² (O)
d/dx(sen-1x) = 1/√1 – x²

Derivada de arcsin Prueba por la regla de la cadena

Para encontrar la derivada de arcsin utilizando la regla de la cadena, supongamos que y = arcsin x. Tomando sin en ambos lados,

sin y = sin (arcsin x)

Por la definición de función inversa, sin (arcsin x) = x. Así que la ecuación anterior se convierte en

sin y = x … (1)

Diferenciando ambos lados con respecto a x

d/dx (sen y) = d/dx(x)

Tenemos d/dx (sen x) = cos x. Además, por la regla de la cadena

cos y – dy/dx = 1

dy/dx = 1/cos x

Utilizando una de las identidades trigonométricas, cos y = √1 – sin²y = √1 – x² (de (1))

Así que dy/dx = 1/√1 – x²

Volviendo a poner y = arcsin x

d/dx (arcsin x) = 1/√1 – x²

Por lo tanto, se ha demostrado.

Ejemplos resueltos utilizando la derivada de arcsin x

Encontrar la derivada de y = arcsin (1/x).

Solución:

Sea f(x) = arcsin (1/x).

Sabemos que d/dx (arcsin x) = 1/√1 – x².

Además, por la regla de la cadena,

y’ = 1/√(1 – (1/x)² – d/dx (1/x)

= 1/ √(1 -(1/x²) – (-1/x2)

= x/√x² – 1 – (-1/x2)

= (-1) / (x√x² – 1)

Respuesta: La derivada de la función dada es (-1) / (x√x² – 1).

Hallar la derivada de y = sen-1(1 + x2).

Solución:

Sea f(x) = sin-1(1 + x2).

Sabemos que d/dx (sin-1 x) = 1/√1 – x².

Además, por la regla de la cadena

y’ = 1/√1 – (1+ x²)² – d/dx (1 + x2)

= 1 / √1 – 1 – x⁴ – 2x² – (2x)

= (2x) / √- x⁴ – 2x²

= (2x) / √x²(- x² – 2)

= 2 / √-x² -2

Respuesta: La derivada de la función dada es 2 / √- x² – 2.

Hallar la derivada de y = x arcsin x.

Solución:

La función dada es, y = x arcsin x.

Es un producto. Así que usamos la regla del producto para encontrar su derivada.

y’ = x – d/dx (arcsin x) + arcsin x – d/dx (x)

= x [1/√1-x²] + arcsin x (1)

= x/√1-x² + arcsin x

Respuesta: La derivada de la función dada es x/√1-x² + arcsin x.

Vídeos de Derivada del arcoseno

Contenido