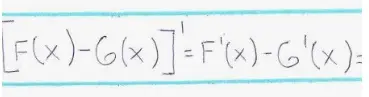Derivada de una resta
Cuando tomamos la derivada, por ejemplo de la función f(x)=x+3, solemos decir que estamos tomando la derivada de y=f(x) con respecto a x, o cualquiera que sea la variable independiente (más adelante tomaremos la derivada con respecto a más de una variable). Cuando tomamos la derivada respecto a x, podemos verla escrita de las siguientes maneras: f′(x),y′,dydx,d(f(x))dx,ddx(f(x)) (y se puede ver de otra manera, como dfdx,ddxy,Dxy). Todo significa básicamente lo mismo.
Ten en cuenta que cuando tienes una expresión algebraica que es una suma o una diferencia (como x2+x+3), puedes separar las expresiones y tomar la derivada de cada parte (como x2 y x y 3) y sumarlas (o restarlas). Esto se llama la regla de la suma y la diferencia.
Regla de la constante
Esta es fácil; siempre que tengamos una constante (un número por sí mismo sin una variable), la derivada es simplemente 0. Por ejemplo, si tenemos y=3 y queremos la derivada de esa función, es simplemente 0.
d/dx(c)=0
Regla de la potencia
La regla de la potencia consiste en tomar el exponente de una función y moverlo al frente (para multiplicar el resto por, incluyendo cualquier coeficiente), y luego bajar el exponente un nivel. Sin embargo, para poder utilizarla, tenemos que asegurarnos de que es sólo x (o la variable que sea) la que se eleva a ese exponente.
Por ejemplo, si tenemos y=4×3, movemos el 3 delante, y bajamos la x al cubo a x al cuadrado: dydx=3⋅4×3-1=12×2. Curiosamente, cuando tomamos la derivada del volumen de una esfera con respecto a su radio, V=43πr3, obtenemos la superficie de una esfera, dVdr=3⋅43πr3-1=4πr2.
Regla del producto
La regla del producto se complica un poco más, pero después de un rato, la harás en sueños. Hazla en una pequeña canción, y se vuelve mucho más fácil. Y fíjate en que normalmente tienes que usar las reglas de la constante y de la potencia para las expresiones individuales cuando estás usando la regla del producto.
Sólo usa la regla del producto si hay algún tipo de variable en las dos expresiones que estás multiplicando. Por ejemplo, úsala cuando tengas algo como x2(x+3), pero no algo como (5×2)(2); convierte esto en 10×2.
También, si puedes, puedes convertir los exponentes de la parte inferior en exponentes negativos; por ejemplo, 5×2=5x-2 .
Intenta simplificar tu función primero.
Y ten en cuenta que cuando tienes el producto de dos expresiones con variables en él, la derivada no es sólo el producto de sus derivadas.
Esto es lo que parece en forma de teorema:
El producto de dos funciones diferenciables es diferenciable y es:
ddx(f(x)⋅g(x))=f(x)g′(x)+g(x)f′(x)
Regla del cociente
En primer lugar, recuerda que no necesitas utilizar la regla del cociente si sólo hay números en la parte inferior, ¡sólo si hay variables en la parte inferior (en el denominador)!
Una cosa que hay que recordar sobre la regla del cociente es que siempre hay que empezar por la parte inferior, y entonces será más fácil. Yo lo recuerdo así: Abajo por la derivada de arriba menos arriba por la derivada de abajo, todo sobre el fondo al cuadrado. Fíjate que en la parte superior hay un menos, no un más.
Ten en cuenta que si puedes separar un cociente en términos individuales, es mejor evitar la regla del cociente. Por ejemplo, si tienes la función f(x)=x3+3x, es mejor dividir ambos términos de la parte superior entre x para obtener f(x)=x2+3x=x2+3x-1
También hay que tener en cuenta que normalmente se puede convertir cualquier función que parezca un cociente en un producto, utilizando exponentes negativos. Algunos prefieren no utilizar nunca la regla del cociente, sino la del producto. Pero a medida que practiques la diferenciación, encontrarás el método que mejor te funcione.
Vídeos de Derivada de una resta
Contenido